Partial Derivatives and OLS Regression

7.10. Partial Derivatives and OLS Regression#

Ordinary least squares (OLS) regression of 2-dimensional data is an important concept in data analysis. Given a collection of data points

\[(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\]

the goal is to find a line \(y=mx+b\) (called the OLS regression line) that best fits the data in the sense that it minimizes the sum of square vertical separations between the data points and the line:

\[ S(m,b) =(y_1-(mx_1+b))^2 + (y_2-(mx_2+b))^2 + ... + (y_n-(mx_n+b))^2.\]

The optimal values of \(m\) and \(b\) minimize \(S(m,b)\), and hence may be obtained using a system of two equations and 2 unknowns:

\[\frac{\partial S}{\partial m} = 0 \]
\[\frac{\partial S}{\partial b} = 0 \]

Example

Consider the data values (1,1), (2,3), and (4,3). In this case,

\[ S(m,b)= (m+b-1)^2 + (2m+b-3)^2+(4m+b-3)^2.\]

This gives rise to the system

\[\frac{\partial S}{\partial m} = 2(m+b-1)+2(2m+b-3)(2)+2(4m+b-3)(4)=42m +14b-38=0 \]
\[\frac{\partial S}{\partial b} = 2(m+b-1)+2(2m+b-3)+2(4m+b-3)=14m+6b-14=0. \]

The system is equivalent to

\[21m +7b=19 \]
\[7m+3b=7. \]

We can solve this system by multiplying the first equation through by 3, and the second equation through by 7

\[63m +21b=57 \]
\[49m+21b=49. \]

Subtracting the second equation from the first equation gives

\[14m= 8 \Rightarrow m=\frac{4}{7}. \]

We find \(b\) by back substitution:

\[7(4/7) + 3b = 7 \Rightarrow 3b=3 \Rightarrow b=1. \]

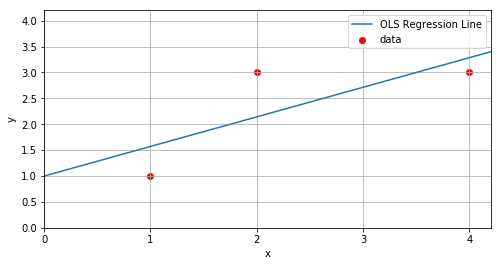
The plot below shows the OLS regression line \(y=\frac{4}{7}x+1\) together with the three data points.

Hide code cell source 
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(8, 4))
plt.xlim((0,4.2))
plt.ylim((0,4.2))
#--plot the data points-----
x=[1,2,4] #(x coordinates of the data)
y=[1,3,3] #(y-coordinates of the data)
plt.scatter(x,y,color='r',label='data')
#--plot the OLS regression line-----
m=4/7
b=1
xreg=np.linspace(0,5,50)
yreg=m*xreg+b
plt.plot(xreg,yreg,label="OLS Regression Line")
plt.gca().set_xticks(np.arange(0,5,1))
plt.grid()
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.show()
../../_images/490a4dfb394ab1cde6ed9588a9b9f758b57224f6800163ee61fb183088e258df.png

7.10.1. Exercises#

Exercises

A college admissions officer has compiled the following data relating 8 students’ high school and college GPA:

GPA

High School GPA:

2.0

2.5

3.0

3.0

3.5

3.5

4.0

4.0

College GPA:

1.5

2.0

2.5

3.5

2.5

3.0

3.0

3.5

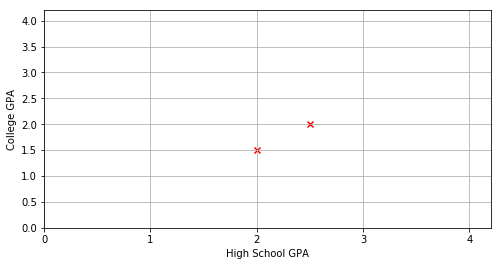
  1. Complete the plot of this data and then guess the value of \(m\) and \(b\) for the least squares regression line \(y=mx+b\). (Use your guess to check that your answer to problem 2 is reasonable).

Hide code cell source 
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(8, 4))
plt.xlim((0,4.2))
plt.ylim((0,4.2))
hs=[2.0,2.5]
col=[1.5,2.0]
plt.scatter(hs,col,color='r',marker='x')
plt.gca().set_xticks(np.arange(0,5,1))
plt.grid()
plt.xlabel("High School GPA")
plt.ylabel("College GPA")
plt.show()
../../_images/29524645917e711e05367c8b56674ecc5ff374f01326a3bb3981c5f369d7b318.png

Exercises (continued)

  1. Use calculus to find the least squares regression line \(y=mx+b\).

  2. Use the second derivative test to verify the choice of \(m\) and \(b\) in problem 2 that gives a minimum for the sum of squares \(S(m,b)\).

  3. Use the regression line to predict the college GPA’s:

GPA

High School GPA:

2.0

3.0

4.0

College GPA:

Contents