10.6. Solution to Exercises

10.6.1. OLS Linear Regression

Problem 1) The system is

\[\begin{align*} a+b&=0,\\ a + 4b&=5,\\ a+7b&=8; \end{align*}\]

or, in matrix form,

\[\begin{align*} \begin{pmatrix} 1& 1\\ 1& 4\\ 1&7\\ \end{pmatrix} \begin{pmatrix} a\\ b\\ \end{pmatrix}= \begin{pmatrix} 0\\ 5\\ 8\\ \end{pmatrix}. \end{align*}\]

The normal equations are

\[\begin{align*} \begin{pmatrix} 1& 1&1\\ 1&4&7\\ \end{pmatrix} \begin{pmatrix} 0\\ 5\\ 8\\ \end{pmatrix}= \begin{pmatrix} 1& 1&1\\ 1&4&7\\ \end{pmatrix} \begin{pmatrix} 1& 1\\ 1& 4\\ 1&7\\ \end{pmatrix} \begin{pmatrix} a\\ b \end{pmatrix}, \end{align*}\]

or

\[\begin{align*} \begin{pmatrix} 13\\ 76 \end{pmatrix}= \begin{pmatrix} 3&12\\ 12&66 \end{pmatrix} \begin{pmatrix} a\\ b \end{pmatrix}. \end{align*}\]

Solving the normal equations gives the least-squares solution \(a=-1\), \(b=4/3\).

Problem 2)

The system is

\[\begin{align*} a-b+c&=1,\\ a&=0,\\ a+b+c&=2,\\ a+2b+4c&=3;\\ \end{align*}\]

or, in matrix form,

\[\begin{align*} \begin{pmatrix} 1& -1&1\\ 1& 0&0\\ 1&1&1\\ 1& 2&4 \end{pmatrix} \begin{pmatrix} a\\ b\\ c \end{pmatrix}= \begin{pmatrix} 1\\ 0\\ 2\\ 3 \end{pmatrix}. \end{align*}\]

The normal equations are

\[\begin{align*} \begin{pmatrix} 1& 1&1&1\\ -1&0&1&2\\ 1&0&1&4 \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 2\\ 3 \end{pmatrix}= \begin{pmatrix} 1& 1&1&1\\ -1&0&1&2\\ 1&0&1&4 \end{pmatrix} \begin{pmatrix} 1& -1&1\\ 1& 0&0\\ 1&1&1\\ 1& 2&4 \end{pmatrix} \begin{pmatrix} a\\ b \end{pmatrix}, \end{align*}\]

or

\[\begin{align*} \begin{pmatrix} 6\\ 7\\ 15 \end{pmatrix}= \begin{pmatrix} 4&2&6\\ 2&6&8\\ 6&8&18 \end{pmatrix} \begin{pmatrix} a\\ b\\ c \end{pmatrix}. \end{align*}\]

Solving the normal equations gives the least-squares solution \(a=3/5, b=3/10\), and \(c=1/2.\)

10.6.2. K-means clustering

Problem 1) \(\mathbf{w}_1=(-4,-1.2)\), \(\mathbf{w}_2=(-3.2,-0.72)\) and \(\mathbf{w}_3=(-2.56,-0.432)\). The gradient descent sequence will converge to the minimum point at \((0,0)\). To prove this, note that if we let \(\mathbf{w}_n=(x_n,y_n)\), then \(\mathbf{w}_n=\mathbf{w}_{n-1}-0.1\nabla \mathbf{w}_{n-1}\) implies that \(x_n=0.8x_{n-1}\) and \(y_n=0.6y_{n-1}\). It follows that \(\lim_{n\rightarrow \infty} x_n=\lim_{n\rightarrow \infty} y_n=0.\)

Problem 2)

i)Fix the prototypes \(z_1=(-1,0)\) and \(z_2=(1,0)\). Then we have \(y_{1,1}=1\), \(y_{1,2}=0\), \(y_{2,1}=1\), \(y_{2,2}=0\), \(y_{3,1}=1\), \(y_{3,2}=0\), \(y_{4,1}=0\), \(y_{4,2}=1\), \(y_{5,1}=0\), \(y_{5,2}=1\), \(y_{6,1}=0\), \(y_{6,2}=1\).

ii) Fix each of these assignments, then the prototypes are unchanged: \(\mathbf{z}_1=(-1,0)\), \(\mathbf{z}_2=(1,0)\).

iii) Fix the prototypes and the assignments are as before.

Thus, the points \((-1,-1)\), \((-1,0)\), \((-1,1)\) are assigned to cluster 1, and the points \((1,-1)\), \((1,0)\), and \((1,1)\) to cluster 2.

Problem 3)

i) Fix the prototypes \(z_1=(-1,0)\) and \(z_2=(1,0)\). Then we have \(y_{1,1}=1\), \(y_{1,2}=0\), \(y_{2,1}=1\), \(y_{2,2}=0\), \(y_{3,1}=1\), \(y_{3,2}=0\), \(y_{4,1}=0\), \(y_{4,2}=1\), \(y_{5,1}=0\), \(y_{5,2}=1\), \(y_{6,1}=0\), \(y_{6,2}=1\).

ii) Fix each of these assignments, then the prototypes are unchanged: \(\mathbf{z}_1=(-1,0)\), \(\mathbf{z}_2=(1,0)\).

iii) Fix the prototypes and the assignments are as before.

Thus, the points \((-1,-1)\), \((-1,0)\), \((-1,1)\) are assigned to cluster 1, and the points \((1,-1)\), \((1,0)\), and \((1,1)\) to cluster 2.

Problem 4)

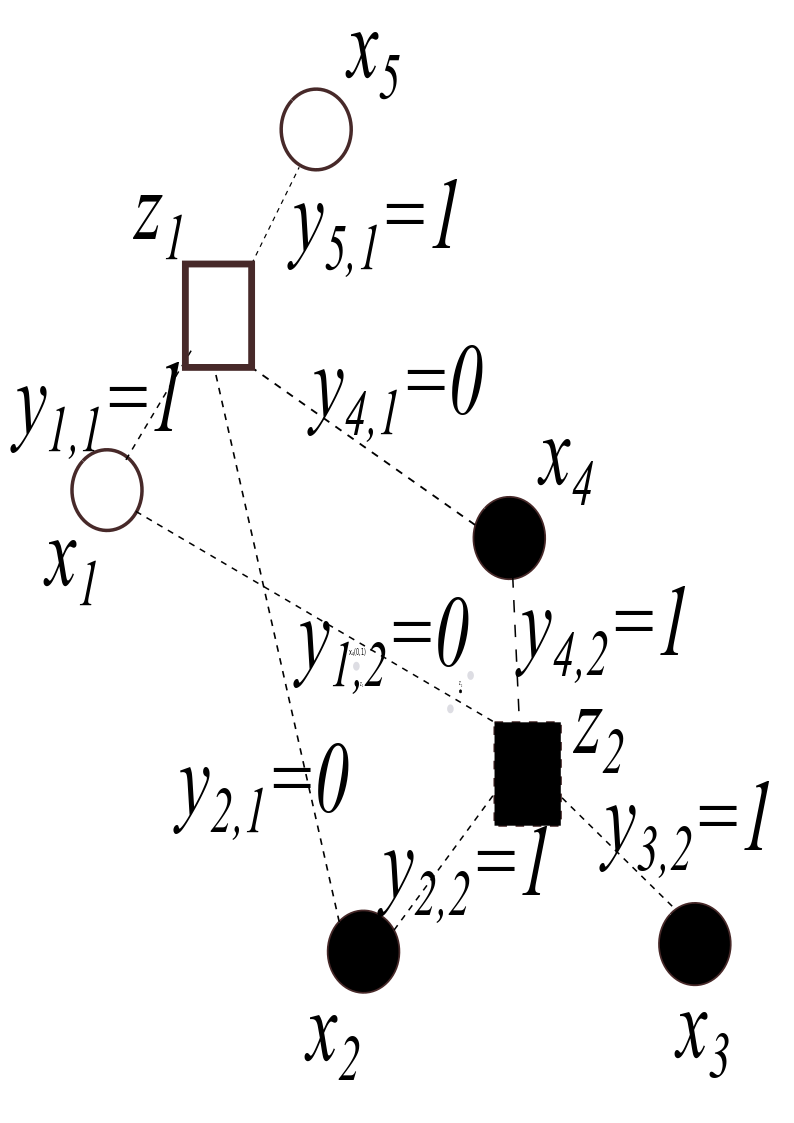
10.6.3. Dimension Reduction by PCA

a)

The data matrix is

\[\begin{align*} \mathbf{X}= \begin{pmatrix} -1 & 3\\ 0& 0 \\ 1&-3 \end{pmatrix}. \end{align*}\]

The covariance matrix is

\[\begin{align*} \mathbf{V}=\frac{1}{3} \begin{pmatrix} 2 & -6 \\ -6 & 18\\ \end{pmatrix}= \begin{pmatrix} 2/3 & -2 \\ -2 & 6\\ \end{pmatrix} \end{align*}\]

Thus, \(Var(\mathbf{x})=2/3\), \(Var(\mathbf{y})=6\), and \(Cov(\mathbf{x},\mathbf{y})=-2.\)

b) \(\,\)The eigenvalues are 0 and 10. The principal component is determined by the largest eigenvalue \(\lambda=10\), which has eigenvector \((1,-3).\) This vector determines the line \(y=-3x,\) which is the desired line.

a)

\[\begin{align*} \scriptsize \mathbf{A}= \begin{pmatrix} 2 & 2 & 0 \\ 2 & 2 & 0 \\ 0 & 0 & 1/2 \end{pmatrix}. \end{align*}\]

b)

The eigenvalues of \(\mathbf{A}\) are \(\lambda_1=4\), \(\lambda_2=1/2\), \(\lambda_3=0\), with corresponding unit eigenvectors for \(\mathbf{v}_1=(1/\sqrt{2},1/\sqrt{2},0)^T\), \(\mathbf{v}_2=(0,0,1)^T\), and \(\mathbf{v}_3=(1/\sqrt{2},-1/\sqrt{2},0)^T\)

The first principal component of \(\mathbf{X}\) is given by \(\lambda_1,\mathbf{v}_1\), the second principal component of is given by \(\lambda_2,\mathbf{v}_2\), and the third principal component is given by \(\lambda_3,\mathbf{v}_3\).

c)

The variance of the data along the line through the origin determined by \(\mathbf{v}_1\) is the maximum among all lines through the origin.

The total variance of the data (sum of squared distances to the origin) is the sum of the variances by projecting the data onto the three lines through the origin determined by the mutually orthogonal unit vectors \(\mathbf{v}_1\), \(\mathbf{v}_2\), and \(\mathbf{v}_3\).

The variances along each of these lines decrease. Each captures more of the variance in an optimal way. The first principal component captures the most amount of variance projecting the data onto a line through the origin (1D subspace). This line is determined by \(\mathbf{v}_1\). The first two principal components capture the most variance if the data is projected onto a plane through the origin (2D subspace): the plane is determined by the vectors \(\mathbf{v}_1\) and \(\mathbf{v}_2\).

a) \(\,\) By inspection, the greatest variance occurs in the \(y\)-coordinate, so we expect the first principal component to be in the direction of the line determined by \((0,1,0)\). In the orthogonal direction (i.e., the \(xz\)-plane), we see that the data lie on the line \(x=2z\). Thus, we expect the second principal component to be in the direction of the line determined by \((2,0,1)/\sqrt{5}\).

b) \(\,\)

\[\begin{split} \mathbf{A}= \begin{pmatrix} 2 & 0 & 1 \\ 0 & 8 & 0 \\ 1 & 0 & 1/2 \end{pmatrix}. \end{split}\]

The first principal component is given by \(\lambda_1=8\) with eigenvector \((0,1,0)\).

The second principal component is given by eigenvector \(\lambda_2=5/2\) with eigenvector \((2,0,1)/\sqrt{5}\).

a) \(\,\) The line along which the projected points have the greatest variance.

b) \(\,\) There is a difference in the outliers–of significance in considering the most vulnerable.

a) \(\,\) The original image is represented by a vector in \(\mathbf{R}^{32^2}=\mathbf{R}^{1024}\) where each pixel value corresponds to a coefficient in the standard basis. The PCA image can be represented using just 2 coefficients corresponding to the first two PCA basis vectors.

b) If we used the standard basis, we would get the grayscale values for two of the \(64^2\) pixels, and the rest of the pixels would have a value of 0 (i.e., appear as pure black.) There would be no way to distinguish whether the letter is an ‘a’ or ‘b’ using just two coordinates in the standard basis.

10.6.4. Binary Classification by SVM

a) \(\,\) The hyperplane is the line \(x_1+2x_2=1\)

b) \(\,\) The two half-spaces are the half-plane \(\pi^+: x_1+2x_2>1\) and the half-plane \(\pi^-: x_1+2x_2<1.\)

a) \(\,\) For any \(k\neq 0\), we have\( \mathbf{w}\cdot\mathbf{x}+b=0\) if and only if \( k(\mathbf{w}\cdot\mathbf{x}+b)=0\) if and only if \( k\mathbf{w}\cdot\mathbf{x}+kb=0\)

b) \(\,\) The signed distance formula is \(\rho(\mathbf{x},\pi)=\frac{\mathbf{w}\cdot\mathbf{x}+b}{\|\mathbf{w}\|}\). Since \(\mathbf{w}\cdot\mathbf{0}=0,\) the signed distance is \(\mathbf{\rho}(\mathbf{0},\mathbf{\pi})= \frac{b}{\|\mathbf{w}\|}\).

c) \(\,\) As in the right panel of the 4th figure in “Intuition Underlying SVM”, there are infinitely many parallel separating hyperplanes with the same margin filling in the space between support vectors. The SVM hyperplane is the one that is equidistant from the two classes \(C_1, C_2.\)

d) \(\,\) The SVM \(L_2\) loss function simplifies to \(J=\frac{\lambda}{2}\|\mathbf{w}\|^2\) (\(\lambda>0\)), which if minimized will then maximize the margin \(\frac{2}{\|\mathbf{w}\|}\).

3. See the JNB Support Vector Machines.