import math
import numpy as np
import matplotlib.pyplot as plt
import random
random.seed()

5.6. Random Walks

A random walk on the number line is a path in which each of \(n\) steps is taken either to the left or right at random. In an unbiased random walk, each step has a 50-50 chance of going to the left or to the right.

A random walk on a square lattice is a path in which each of \(n\) steps is taken left, right, up, or down at random. In one example of a biased random walk, a person takes a step left with probability 0.35, a step right with probability 0.2, a step forward with probability 0.4, and a step back with probability 0.05. Note the probabilities add to 1, meaning there are no other options at each iteration.

A random walk is an example of a stochastic process because it yields varied output due to randomness when it is executed repeatedly with the same input. By contrast, a deterministic process yields the same output when it is executed repeatedly with the same input. Random walks can be used to model (describe) practical processes in a variety of areas of study, such as the motion of particles in physics, changes in DNA and “genetic drift” in biology, the changes in stock prices in financial markets, and human migration and relocation in global geography and societies.

In a traditional framing of a random walk, a drunk person walks on a street with an equal probability of movement to the left or right at each pace. One can readily ask many questions about the random walk that can be surprisingly challenging to answer via basic calculation and pencil-and-paper experimentation.

For instance, in an unbiased random walk on the number line, what is the expected number of paces the person should take in order to move one pace to the left of the starting point? Also consider, in the example above of the biased random walk on a square lattice, what is the expected number of paces the person should take in order to visit the location one pace to the left of the starting point?

Mathematical approaches can provide answers about random walks. However, many questions prove quite difficult to address theoretically.

Computer simulations can conveniently and intuitively provide insights into random walks. They can also illustrate the variations that occur over many trials of an experiment. In this section, we use computation to consider the questions above and more.

Example: Consider and explore this Python code for a random walk on a square lattice. We see a possible output below.

n = 1000
x, y = np.zeros(n), np.zeros(n)
for i in range(1, n):
    val = random.choice(['forward', 'back', 'left', 'right'])
    if val == 'forward':
        x[i] = x[i-1]
        y[i] = y[i-1] + 1
    elif val == 'back':
        x[i] = x[i-1]
        y[i] = y[i-1] - 1
    elif val == 'left':
        x[i] = x[i-1] - 1
        y[i] = y[i-1]
    else: # val == 'right'
        x[i] = x[i-1] + 1
        y[i] = y[i-1]
plt.plot(x, y, 'r*-')
plt.title(f"{n} steps")
plt.show()
print(f"Final position: {x[n-1]}, {y[n-1]}")

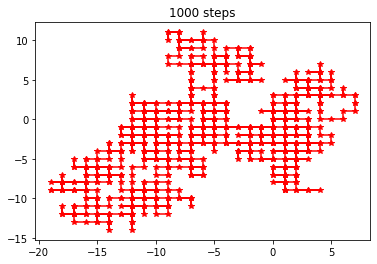
Final position: -10.0, 1.0

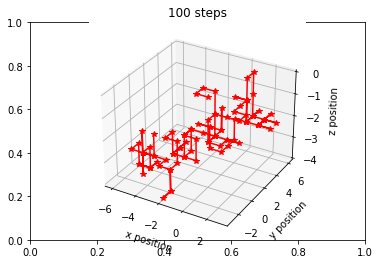
Example: Consider and explore this Python code for a random walk on a cubic lattice! We see a possible output below.

n = 100
x, y, z = np.zeros(n), np.zeros(n), np.zeros(n)
for i in range(1, n):
    val = random.choice(['forward', 'back', 'left', 'right', 'up', 'down'])
    if val == 'forward':
        x[i] = x[i-1]
        y[i] = y[i-1] + 1
        z[i] = z[i-1]
    elif val == 'back':
        x[i] = x[i-1]
        y[i] = y[i-1] - 1
        z[i] = z[i-1]
    elif val == 'left':
        x[i] = x[i-1] - 1
        y[i] = y[i-1]
        z[i] = z[i-1]
    elif val == 'right':
        x[i] = x[i-1] + 1
        y[i] = y[i-1]
        z[i] = z[i-1]
    elif val == 'up':
        x[i] = x[i-1]
        y[i] = y[i-1]
        z[i] = z[i-1] + 1
    else: # go down
        x[i] = x[i-1]
        y[i] = y[i-1]
        z[i] = z[i-1] - 1
plt.title(f"{n} steps")
ax = plt.axes(projection='3d')
ax.set_xlabel('x position')
ax.set_ylabel('y position')
ax.set_zlabel('z position')
plt.plot(x, y, z, 'r*-')
print(f"Final position: {x[n-1]}, {y[n-1]}, {z[n-1]}")

Final position: -4.0, -1.0, -2.0

Note you can change the figure size, for example by inserting the following line before plotting:

fig = plt.figure(figsize = (10, 10), dpi = 50)

<Figure size 500x500 with 0 Axes>

5.6.1. Exercises

Exercises

Exercise 1: A person walks on a street with an equal probability of movement to the left or right at each pace. Write a Python program to approximate the expected number of paces the person should take in order to move one pace to the left of the starting point. Suggestion: Use 0 as the starting point. State your conclusions in a complete sentence.

Exercise 2: Consider an unbiased random walk on a square lattice. Write a Python program to find approximate answers to the following questions:

(a) What is the expected number of a paces the person should take in order to visit the location one pace to the left of the starting point (0, 0)? Explain.

(b) How far away from the starting point (0,0) does a person end up after \(n\) steps of an unbiased random walk on a square lattice? Explain.

(c) If you run the simulation program for Part (b) many times, is there any statistical distribution you can expect? Explain.

Exercise 3: A person walks one pace left with a probability of 0.35, one pace right with a probability of 0.2, one pace forward with a probability of 0.4 and one pace backward with a probability of 0.05. Write a Python program to approximate the expected number of paces the person should take in order to visit the location one pace to the left of the starting point. State your conclusions in a complete sentence.

Exercise 4: A person walks one pace left, right, forward or back with equal probability. When the person walks left, right, or back, she walks one pace. When she walks forward, she walks two paces. Write a Python program to approximate how far forward the person has walked in 1000 paces. State your conclusions in a complete sentence.

Exercise 5: A Markov chain describes a sequence of possible events in which the probability of each event depends on the state in the previous event. For example, suppose that we modify an unbiased random walk on a square lattice such that if the previous step was to the right, then the probability of making the current move up, down, left, or right is 0.2, 0.2, 0.4, or 0.2, respectively. As such,

(a) explain the implications of a move to the right in practical terms in a complete sentence.

(b) run some simulations and address the question: How does the use of the Markov chain change the unbiased random walk on a square lattice?

Exercise 6: Two people get lost in a shopping mall. They both want to find each other as soon as possible. However, each has no clue where the other one is. There are two strategies available:

(1) One person stays in the same place. The other moves around.

(2) Both people move.

Which strategy is better for them to meet?

Do simulations and explain how they support your answer.