13.2. Complex Analysis Background#
13.2.1. The Complex Function \(f(z)\)#
A complex function \(w=f(z)\) maps a complex number \(z\in \mathbb{C}\) to a complex number \(w\in\mathbb{C}\) where the set of complex numbers, \(\mathbb{C}\), is defined as
where \(\mathbb{R}\) denotes the set of real numbers. Basic arithmetic operations in \(\mathbb{C}\) include:
Addition and Subtraction: \(\, z_1\pm z_2=(x_1+iy_1)\pm (x_2+iy_2) = (x_1\pm x_2)+i(y_1 \pm y_2)\);
Multiplication: \(\, z_1z_2=(x_1+iy_1)(x_2+iy_2)=x_1x_2-y_1y_2+i(x_1y_2+x_2y_1)\); and
Division: \(\frac{z_1}{z_2}=\frac{x_1+iy_1}{x_2+iy_2}=\frac{(x_1+iy_1)(x_2-iy_2)}{(x_2+iy_2)(x_2-iy_2)}=\frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+i\frac{x_2y_1-x_1y_2}{x_2^2+y_2^2}\) .
Each complex number \(z=x+iy\) is identified with a point \(z=(x,y)\) in the Cartesian plane as shown in the figure below.
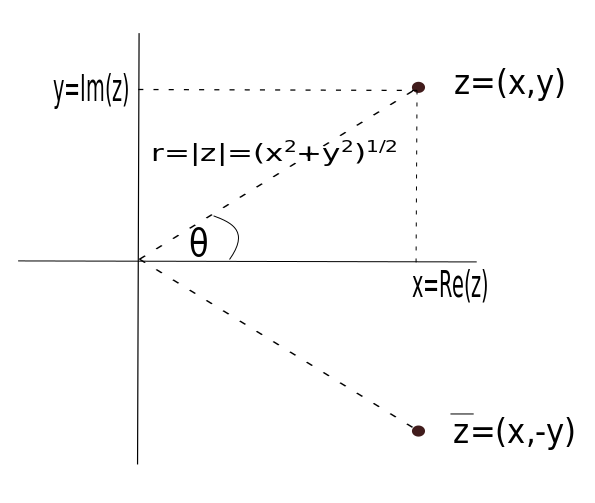
We call \(x=Re(z)\) the real part of \(z\), and \(y=Im(z)\) the imaginary part. Complex numbers are also expressed in polar or exponential form as \(z=r\,e^{i\theta}\), where \(r=|z|=\sqrt{x^2+y^2}\) is called the modulus of \(z\) and \(\theta=\arctan{\frac{y}{x}}\) is called the argument of \(z\) (denoted \(\arg z\)) . Note that \(|z|\) can be thought of as the ``magnitude” of \(z\), and \(|z_1-z_2|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) the distance between \(z_1=(x_1,y_1)\) and \(z_2=(x_2,y_2)\) as points in the Cartesian plane.
Given a complex number \(z=x+iy\), the number \(\overline{z}=x-iy\) is called the conjugate of \(z\). Note that \(z\,\overline{z}=x^2+y^2\in \mathbb{R}\). Complex conjugates are used in division since multiplication by the reciprocal of \(z\) is multiplication by \(\frac{1}{z}=\frac{\bar{z}}{z \bar{z}}=\frac{x}{x^2+y^2}-i\frac{y}{x^2+y^2}.\)
The output of a complex function \(f:\mathbb{C} \rightarrow \mathbb{C}\) may be expressed as \(f(x+iy)= u(x,y)+iv(x,y)\), where \(u\) and \(v\) are both real-valued functions. For example, if \(f(z)=z^3\), then
In this case, \(u(x,y)=x^3-3xy^2\) and \(v(x,y)=3x^2y-y^3\).
Here are some important elementary complex functions:
Polynomial functions:
\(f(z)=a_0 + a_1z + a_2 z^2 + ... + a_n z^n \) where \(a_i\in\mathbb{C}\) for \(i=0,...,n\) and \(a_n\neq 0\). The value of the whole number \(n\) is called the degree of the polynomial. (\(a_0=0\) is allowed for the special case \(n=0\) when \(f(z)\) is constant.)
Rational functions:
\(f(z)=\frac{P(z)}{Q(z)}\), where \(P\) and \(Q\) are both polynomials and \(Q(z)\neq 0\).
Exponential function:
\(f(z)=e^z\), where \(e\) is Euler’s number (\(e\approx 2.71...\)). Note that \(e^z=e^{x+iy}=e^xe^{iy}= e^x(\cos(y)+ i \sin (y))=e^x\cos(y) + i e^x\sin(y)\), so in this case \(u(x,y)=e^x\cos(y)\) and \(v(x,y)=e^x\sin(y)\). This result follows from Euler’s identity
which can be proven using the Taylor expansion
that is valid for all \(z\in\mathbb{C}\):
The complex logarithm:
\(f(z)=\log(z)\). To define the complex log function \(\log z\), we use the real natural log function \(\ln(\cdot)\) applied to the polar form \(z=re^{i(\theta +2n\pi)}\):
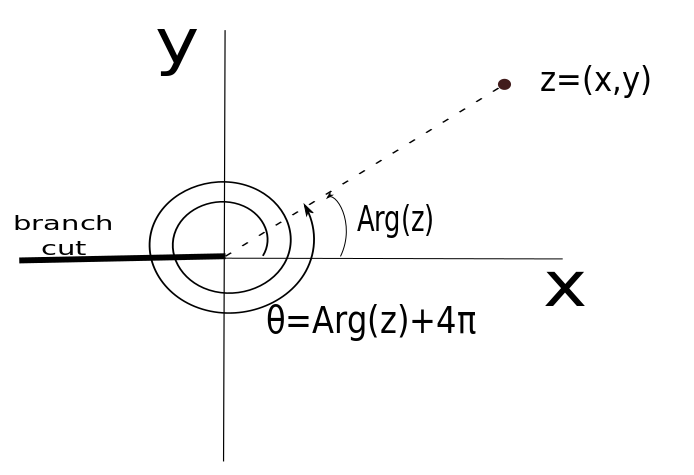
Note that since there are multiple polar representations of the same complex number \(z\), the complex log is multiple valued as well. In order to make a single-valued function, we need to restrict the values of \(\theta\) to an interval of length \(2\pi\) (with one of the endpoints excluded). This restriction is called a branch of the natural log. A branch cut is a ray which determines the branch. The point from which the branch cut emanates is called the branch point. For example, the ray \(\theta=-\pi\) determines a branch \(-\pi < \theta \le \pi\). This branch is called the principal branch and the principal value is denoted Log \(z\) (note the capital L):
where \(-\pi < Arg\, z \le \pi\).
The figure below shows the argument of \(z\) given by \(\theta = \arg(z)=Arg\, z+ 2n\pi\) for the case \(n=2\)
Exercises#
Exercises
2.1.1 Let \(x=2+3i\) and \(y=-1+5i\). Calculate the following:
a) \(x+y\)
b) \(x-y\)
c) \(xy\)
d) \(\frac{x}{y}\)
e) \(x\bar{y}\)
2.1.2 Express the following complex functions in the form \(u(x,y)+iv(x,y)\).
a) \(f(z)=e^{2z}\)
b) \(g(z)= \log (z+1)\)
c) \(h(z)=z^2-1\)
2.1.3 Show that \(|z_1 z_2| = |z_1| |z_2|\).
2.1.4 Does \(\arg(z_1z_2)=\arg(z_1)\cdot \arg(z_2)\)?
13.2.2. The Derivative \(f'(z)\)#
The limit quotient definition of the derivative is
(note that h is complex!)
We emphasize that in order for a complex function \(f(z)\) to be differentiable at \(z_0\), the quotient \((f(z+h)-f(z))/h\) must approach the same value along every path as \(h \rightarrow 0\) including along both the real and imaginary axes.
As one might guess based on the similarity of the definitions, the basic derivative rules from real-variable calculus continue to hold in complex variables. Given that \(f(z)\) and \(g(z)\) are both differentiable, and \(c_1,c_2\) are complex constants,
Linearity \((c_1f(z)+c_2g(z))'=c_1f'(z)+c_2g'(z)\)
Product Rule \((f(z)g(z))'=f(z)g'(z)+g(z)f'(z)\)
Quotient Rule \((\frac{f(z)}{g(z)})'=\frac{g(z)f'(z)-f(z)g'(z)}{[g(z)]^2}\)
Chain Rule \([f(g(z))]'=f'(g(z)) g'(z)\)
Power Rule \(\frac{d}{dz} z^n = n z^{n-1}\), where \(n\) is an integer,
L’Hospital’s Rule \(\lim_{z\rightarrow z_0}\frac{f(z)}{g(z)} =\lim_{z\rightarrow z_0}\frac{f'(z)}{g'(z)}\) for 0/0 indeterminate form limits.
Exercises#
Exercises
2.2.1 Show using the limit definition that \(\frac{d}{dz} (10z^3) = 30z^2\).
2.2.2 Show that the function \(f(z)=\bar z \) is not differentiable.
2.2.3 Find \(\lim_{z\rightarrow i} \frac{z^4-1}{z^8-1}.\)
13.2.3. The Cauchy-Riemann Equations#
The Cauchy-Riemann equations are a pair of partial differential equations that, along with conditions of continuity, are necessary and sufficient conditions for a complex function \(f(z)\) to be differentiable. These equations are fundamental to both the theory and application of complex analysis.
Recall from Section 1 that the limit quotient definition of the derivative is
Assuming that \(f(z)=f(x+iy)=u(x,y)+i v(x,y)\) is differentiable, and \(h=a+ib\), we may compute \(f'(z)\) along any path \((a,b)\rightarrow (0,0)\). In particular, let us choose the paths along the x and y axes:
Along the x-axis (\(h=a\) where \(a\) is real):
Along the y-axis (\(h=bi\), where \(b\) is real):
The Cauchy-Riemann equations are obtained by equating the two expressions for \(f'(z)\):
and
Note that the CR-equations are a necessary condition for differentiability: if \(f(z)\) is differentiable, then the C-R equations must hold. It is also possible to prove that the CR-equations are sufficient for differentiability (see Thm 2.2 in [Sato 2015]). That is, if the C-R equations are satisfied with \(u_x,v_x,u_y\), and \(v_y\) all continuous functions, then \(f(z)\) is differentiable. In other words, assuming sufficient smoothness of \(u(x,y)\) and \(v(x,y)\), the CR equations are both necessary and sufficient conditions for \(f(z)\) to be differentiable.
Polar Form of the Cauchy-Riemann Equations#
We now consider the polar representation \(f(z)=f(re^{i\theta}) = u(r,\theta) + i v(r,\theta)\) and obtain the C-R equations for \(u\) and \(v\) in polar coordinates.
Let \(z=re^{i\theta}\) and let \(w=z+h\). We again evaluate \(f'(z)\) using two different paths \(h\rightarrow 0\) (equivalently \(w\rightarrow z\)).
straight path
\(h\rightarrow 0\) along the straight path \(h= a e^{i\theta}\) (i.e. \(a\rightarrow 0\) where \(a\) is real). In this case
circular path
\(w\rightarrow z\) along the circular path \(w= r e^{i(\theta +b)}\) (\(b\rightarrow 0\) where \(b\) is real). In this case
It follows that the C-R equations in polar form are
Exercises#
Exercises
2.3.1 Use the C-R equations to show that \(f(z)= z^2 \) is differentiable.
2.3.2 Use the C-R equations to show that \(f(z)= \mid z \mid^2 \) is not differentiable.
2.3.3 Use the CR-equations to show that \(f(z)=e^z\) is differentiable, and find its derivative.
2.3.4 Use the polar form of the CR-equations to find \(\frac{d}{dz} \log z.\)
13.2.4. Harmonic Conjugates#
Harmonic functions are extremely important and have a close connection to complex differentiable functions. A real valued function \(g(x,y)\) of the real variables \(x\) and \(y\) is said to be harmonic if its Laplacian is zero:
In other words, \(g\) satisfies the Laplace equation.
Let \(f(z)=u(x,y)+iv(x,y)\) be a differentiable function with \(u(x,y)\) and \(v(x,y)\) both having continuous second partial derivatives. The C-R equation \(u_x=v_y\) differentiated with respect to \(x\) gives \(u_{xx}=v_{xy}\) and the other C-R equation \(u_y=-v_x\) differentiated with respect to \(y\) gives \(u_{yy}=-v_{yx}=-v_{xy}\), (the last equality follows from the equality of mixed partials). Adding these two results together yields
showing that \(u\) satisfies the Laplace equation.
Using similar reasoning, \(v\) must satisfy the Laplace equation as well.
Writing \(f(z)\) in the polar form \(f(z)=u(r,\theta)+i\,v(r,\theta)\), the polar C-R equations imply that both \(u\) and \(v\) satisfy the polar form of the Laplace equation (see Sec 2.4.2 in [Sato 2015]):
and,
This leads us now to the main topic of this section: harmonic conjugates. If the functions \(u\) and \(v\) satisfy the C-R equations for the Cartesian form or polar form, then we say \(v\) is the harmonic conjugate of \(u\). This leads to the result that
f(z)=u+iv is differentiable if and only if v is the harmonic conjugate of u (see Thm 2.4 in [Sato 2015]).
The harmonic conjugate of \(u\) is obtainable as follows:
i) antidifferentiate \(v_y=u_x\) with respect to \(y\) to obtain
where \(t(x)\) is a real function of \(x\) only and \(U_y=v_y\).
ii) differentiate the last equation with respect to \(x\) and use the C-R equation \(v_x=-u_y\) to obtain
iii) Anti-differentiating with respect to x, we obtain \(t(x)\).
Example#
Find the harmonic conjugate of \(u(x,y)=y^3-3x^2y\).
Solution:
First note that \(u\) is harmonic because \(u_{xx}=-6y\) and \(u_{yy}=6y\), so \(u_{xx}+u_{yy}=0\). Hence, we know that \(u\) has a harmonic conjugate, and can find it by following the three steps above:
i) \(v_y= u_x=-6xy \Rightarrow v = -3xy^2 + t(x).\)
ii) \(v_x=-3y^2+t'(x)=-u_y=-3y^2+3x^2 \Rightarrow t'(x)=3x^2\)
iii) \(t(x)=x^3+ C\), and hence \(v=-3xy^2+x^3+ C\) is the harmonic conjugate of \(u\).
It follows that \(f(z)=u+iv=(y^3-3x^2y)+i(-3xy^2+x^3+C)\) is a differentiable function.
Exercises#
Exercises
2.4.1 Determine whether the following functions can be the real parts of differentiable complex functions.
a) \(u_1(x,y)=x^2-y^2\)
b) \(u_2(x,y)= x^2+y^2\)
c) \(u_3(x,y)=x+42\)
d) \(u_4(x,y)=e^x\,\cos y\)
e) \(u_5(x,y)=\sin x+\sin y\)
2.4.2 For the questions to which you answered “yes” in the question above, find the harmonic conjugates.
13.2.5. Orthogonality#
Another important relationship between the real and imaginary parts \(u\) and \(v\) of a differentiable function \(f(z)\) is the orthogonality of their level curves. That is, the families of curves defined by \(u(x,y)=p_1\) and \(v(x,y)=p_2\), where \(p_1\) and \(p_2\) are constants, are orthogonal. We now show this to be the case. Assuming that \(y\) is a function of \(x\), if we differentiate the level curve \(u(x,y)=p_1\) with respect to \(x\), we get
so the slope along this level curve is computable using
Exercises#
Exercises
2.5.1 Let \(\Phi(x,y) = -x\). Determine \(\Psi(x,y)\) such that \(\Omega(z)=\Omega(x+iy)=\Phi(x,y)+i\Psi(x,y)\) is differentiable and explain why \(\Phi(x,y)=c_1\) and \(\Psi(x,y)=c_2\) defines an orthogonal family of curves.
2.5.2 Let \(f(z)=z^2\).
a)Find \(u(x,y)\) and \(v(x,y)\) such that \(f(z)=u(x,y)+iv(x,y)\).
b) Show that the family of curves \(u(x,y)=c_1\), \(v(x,y)=c_2\) are orthogonal.

