import random
import matplotlib.pyplot as plt
5.9. Solution to Exercises#
I tried to pose these questions to ask for human thought by asking the student to judge, think, etc. I intend for the student to address these questions with original thought and by referring to the chapter and any resource explicitly provided in the question, initially without doing outside research.
Many of the exercises have many answers. I have provided some possible answers from my own perspective.
5.9.1. Random Numbers#
Exercise 1. Which statement do you judge to be more accurate? Why?
The computer program selected a number between 1 and 10 at random.
The computer program selected a number between 1 and 10 arbitrarily.
I consider the first statement to be more accurate because the “arbitrary” description allows for a personal preference, often unconscious, to come into play. A computer does not have a personal whim to influence picking some numbers over others, so “random” may be more accurate.
Exercise 2. When a computer program selects a number between 1 and 10, do you think that the choice involves possible preference for some number over others? Support your answer with examples.
According to this chapter, people typically speak of computers generating random numbers. (Technically the computer is doing pseudo-random number generation in which the number is produced by a step-by-step, complicated, but not random, process.) As such, I think that the process does not involve preference for one number over another, unless the programmer has designed the program such that one number is more likely than another to be chosen. For example, if the computer picks a (pseudo-) random number between 1 and 10 in a conventional way, we can assume each of the ten numbers is equally likely to be chosen with no preference for one number over another. However, the programmer could write a program in which 7 is chosen 50% of the time, and the other 50% of the time, 1, 2, 3, 4, 5, 6, 8, 9, or 10 is chosen with equal probability. In this case, the computer’s choice could be said to involve a “preference” for 7 over the other numbers if you use “preference” to mean simply “an advantage”.
Exercise 3: Think of an example of how randomness might be involved in a study investigating a new medicine. Explain how randomness is involved. Could computation, for example using Python, be helpful in the study? Explain your answer.
A study investigating a new medicine might use randomness to place each volunteer into either a group receiving the old medicine or a group receiving the new medicine. Computation could be helpful in analyzing the results because a large number of participants might be involved, and a large amount of data might be collected. Computers are good at doing a large number of detailed calculations quickly.
Exercise 4: Think of an example of how randomness might occur in the natural world. Explain how randomness is involved. Could a computer simulate or mimic a natural process in the context of your example? If so, how could a computer simulation be useful?
Molecules in the air might have slight fluctuations in temperature and position that are influenced by randomness. A computer could simulate how the particles flow and influence weather, maybe by using broader observations, rather than particle-by-particle information. This could be useful in forecasting the weather.
Exercise 5: Think of an example of how randomness might occur in a game. Explain how randomness is involved. Could a computer simulate the game? If so, how could the computer simulation be useful?
Randomness would occur in a game that involves drawing cards from a deck. A computer could simulate the game if it is programmed with the rules of the game. The computer simulation could be useful for investigating whether a certain strategy is effective by using it in many trials of the game.
Exercise 6: Consider a die (plural: “dice”). Do you think that when we roll a physical die, we can be certain that there is an equal chance of the die landing with each of the six sides facing up? Or could there be a bias toward some sides? Explain your thinking. Do you think the outcome of a roll of the physical die could be influenced by the previous roll? Explain your thinking. How could we use a computer program to simulate a die roll? What are some advantages of doing so?
I think that we cannot be certain that a physical die has an exactly equal chance of landing with each of the six sides facing up because slight imperfections in the die could produce a bias toward some sides. If the die is shaken up well before it is released, then the previous roll should not influence how the die lands. We could use a computer to simulate a die roll by having it generate a random number between 1 and 6. One advantage of using a computer simulation is that it could be used to “roll the die” many times in quick succession for purposes of testing out different ideas, such as: If you roll the die many times, you will get a 1 approximately 1/6 of the time.
Exercise 7: Consider the following answer to the question “True or false— An arbitrary choice is made for no special reason”:
“Yes, an arbitrary choice typically refers to a decision or selection that is made without any specific reason or justification. It means that there is no objective or rational basis for choosing one option over another. Arbitrary choices are often made when there is no clear preference or when the decision doesn’t have a significant impact on the outcome. In such cases, people may resort to random selection, personal whim, or other non-logical factors to make a choice.” (ChatGPT, personal communication, June 6, 2023).
Provide a critique for which parts are right (if any). Provide justification for why they are correct. Identify which parts are wrong (if any) and explain what is wrong. Rewrite the answer in your own words with any corrections that are needed. (Retain the citation as with any paraphrased material.) Add an example that you think of yourself to clarify the answer to the true/false question.
This answer is largely correct. When you ask a friend to pick an arbitrary integer between 1 and 10, you are asking them to make a selection without any specific reason or justification. In this scenario, there is only a personal or gut-level basis for choosing one option over another. We only ask a friend to pick a number arbitrarily when there is no “right answer” that they could use find by reasoning through which number to pick. The friend could pick based on personal whim or non-logical factors or even use a random number generated by a computer. The only part of the answer that I consider wrong is that the decision could have a significant impact on the outcome if you say, for example, “Pick an arbitrary integer between 1 and 10, and if you pick the number I wrote down on this card, I’ll give you my lunch.”
Exercise 8: Use the code below to explore Python commands in therandomlibrary. Read the documentation here as desired: https://docs.python.org/3/library/random.html . For eachprintstatement, insert a comment (using#) that describes all the possible numbers that can be generated.
Show code cell source
print(random.randrange(6))
print(random.randrange(6) + 1)
print(random.randrange(1, 7))
print(random.randint(1, 6))
print(random.randrange(0, 10, 2))
print(random.uniform(10, 20))
4
3
5
1
6
19.30733945140265
Show code cell source
# Generate 0, 1, 2, ..., or 5 at random.
print(random.randrange(6))
# Generate 1, 2, 3, ..., or 6 at random.
print(random.randrange(6) + 1)
# Generate 1, 2, 3, ..., or 6 at random.
print(random.randrange(1, 7))
# Generate 1, 2, 3, ..., or 6 at random.
print(random.randint(1, 6))
# Generate 0, 2, 4, 6, or 8 at random.
print(random.randrange(0, 10, 2))
# Generate a decimal number on the interval [10, 20).
print(random.uniform(10, 20))
0
1
5
1
4
13.446055601574948
Exercise 9: Which does a Python program generate: a pseudo-random number or a truly random number? Give an example, and explain why the example is pseudo random or truly random.
A Python program generates pseudo-random numbers even though we call it “random number generation”. For example, if we do print(random.randrange(6)), Python uses mathematical methods to simulate (mimic) randomness when it selects 0, 1, 2, 3, 4, or 5 with equal probability. The example is pseudo random because the number is produced by a step-by-step, complicated, but not random, process.
5.9.2. Probability#
Exercise 1: Do Problem 5 from the beginning of the Probability section mathematically: Suppose you roll a perfect die \(n\) times and keep a record of each outcome. What is the chance or probability that the die lands on 1, 2, 3, 4, 5, and then 6 when rolled six times (\(n=6\))? Use Python to evaluate your answer. Explain your conclusion in a complete sentence.
(1/6)**6
2.1433470507544573e-05
2.14/100_000
2.1400000000000002e-05
The probability of rolling the sequence 1, 2, 3, 4, 5, and then 6 is approximately 2 in 100,000.
Exercise 2: Do Example 5 from the beginning of the Probability section computationally: Suppose you roll a perfect die \(n\) times and keep a record of each outcome. What is the chance or probability that the die lands on 1, 2, 3, 4, 5, and then 6 when rolled six times (\(n=6\))? Do a large number of trials of six rolls of a die and count the number of times the rolls come out as 1 followed by 2, followed by 3, followed by 4, followed by 5, followed by 6. A piece of syntax you may consider using is if (rolls[0] == 1 and rolls[1] == 2 and rolls[2] == 3 and rolls[3] == 4 and rolls[4] == 5 and rolls[5] == 6):. Compare the fraction times you get this pattern to your mathematical answer from the previous exercise in a complete sentence.
Show code cell source
def six_roll_trials(num_trials):
'''Return the number of times that six rolls of a six-sided die produce the sequence 1, 2, 3, 4, 5, and then 6.'''
rolls = []
count = 0
for i in range (num_trials):
for j in range(6):
rolls.append(random.randrange(6)+1)
if (rolls[0] == 1 and rolls[1] == 2 and rolls[2] == 3 and rolls[3] == 4 and rolls[4] == 5 and rolls[5] == 6):
count = count + 1
rolls = []
return count
def repeat_trials(reps):
'''Print the number of times that six rolls of a six-sided die produce the sequence 1, 2, 3, 4, 5, and then 6
in 100,000 trials, and print the average number of such sequences over reps repetitions of 100,000 trials.'''
count = 0
num_successes = 0
for i in range(reps):
num_successes = six_roll_trials(10**5)
print(num_successes)
count = count + num_successes
print(count/reps)
repeat_trials(10)
2
2
0
2
1
4
4
2
3
4
2.4
When I use my program to do six coin flips 100,000 times, my mathematical answer says I should get the sequence 1, 2, 3, 4, 5, 6 approximately twice. Often I do get 2 “successes” when I do 100,000 trials. Sometimes I get 0 or 1 or sometimes as many as 6 or so, but typically if I do 100,000 trials ten times, the average number of successes is close to the predicted 2.14.
Exercise 3: If event \(A\) is that the die comes up 2, and event \(B\) is that the die comes up with an even number, are the two events \(A\) and \(B\) mutually exclusive? Explain. Is the addition rule \(P(A \ \text{or} \ B) = P(A) + P(B)\) applicable? If so, show that the rule holds. If not, show that the rule does not hold. Use Python to illustrate your answer.
The events are not mutually exclusive because they can happen at the same time. If the die comes up 2, then then the die comes up with an even number. Therefore, the addition rule does not apply. In this case:
# P(A)
pA = 1/6
# P(B)
pB = 3/6
# P(A or B) = P(B) = 1/2, not P(A) + P(B)
pA + pB
# which is approximately
0.6666666666666666
Exercise 4: Calculate the probability (a) mathematically and (b) computationally of obtaining the given result in \(n\) rolls of a fair six-sided die. Make a statement in a complete sentence about how many times you expect the outcome, in terms of a number of trials (consisting of \(n\) rolls per trial). Compare the fraction of times your simulation produces the target pattern with your mathematical answer.
\(n=6\), all numbers are the same
\(n=6\), at least one number is different
\(n=1\), the number rolled is greater than 2
\(n=2\), the sum of the two numbers is greater than 2
\(n=2\), the two numbers are different
\(n=3\), two numbers are the same and one is different
\(n=6\), all the numbers are different
\(n=100\), all the numbers are the same
\(n=6\), the number 1 appears at least once
\(n = 6\), the number 1 appears at most once
# (1.)
# (a)
print("For n = 6 rolls of a fair six-sided die, the probability of getting all the numbers of the same is:")
print("(1/6)**5:")
print((1/6)**5)
print("or approximately once in 10,000 trials: 1.3/10_000:")
print(1.3/10_000)
For n = 6 rolls of a fair six-sided die, the probability of getting all the numbers of the same is:
(1/6)**5:
0.00012860082304526745
or approximately once in 10,000 trials: 1.3/10_000:
0.00013000000000000002
Exercise 4 Part 1b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def six_rolls_all_same_trials(num_trials, n):
'''Return the number of times that n rolls of a six-sided die produce all the same number.'''
rolls = []
count = 0
for i in range (num_trials):
all_same = False
for j in range(n):
rolls.append(random.randrange(6)+1)
for j in range(n):
if rolls.count(j) == n:
all_same = True
if all_same:
count = count + 1
rolls = []
return count
def repeat_trials(reps, n):
'''Print the number of times that n rolls of a six-sided die produce the same number in 10,000 trials,
and print the average number of such sequences over reps repetitions of 100,000 trials.'''
count = 0
num_successes = 0
for i in range(reps):
num_successes = six_rolls_all_same_trials(10**4, n)
print(num_successes)
count = count + num_successes
print(f"Average: {count/reps}")
print("How many times to we get all the numbers the same in 10,000 trials when we do 10,000 trials ten times?")
repeat_trials(10, 6)
How many times to we get all the numbers the same in 10,000 trials when we do 10,000 trials ten times?
2
3
2
0
1
2
1
1
2
0
Average: 1.4
On average we get all the numbers the same around 1 or 2 times in 10,000 trials as expected.
# (2.)
# (a)
print("For n = 6 rolls of a fair six-sided die, the probability of getting at least one number different is")
print("1 - (1/6)**5:")
print(1 - (1/6)**5)
print("or approximately once in 10,000 trials we do NOT get at least one number different.")
print("To check: Summing the answer with the previous answer gives approximately 1:")
print(1 - (1/6)**5 + 1.3/10_000)
For n = 6 rolls of a fair six-sided die, the probability of getting at least one number different is
1 - (1/6)**5:
0.9998713991769548
or approximately once in 10,000 trials we do NOT get at least one number different.
To check: Summing the answer with the previous answer gives approximately 1:
1.0000013991769547
Exercise 4 Part 2b)
The simulation in (a) shows that on average we only get all the numbers the same around 1 or 2 times in 10,000 trials as expected. The rest of the time we get at least one number different from what we expected.
# (3.)
# (a)
print("For n = 1 roll of a fair six-sided die, the number rolled is greater than 2 with probability:")
print("(4/6):")
print(4/6)
print("or approximately 2/3 of the trials:")
print(2/3)
For n = 1 roll of a fair six-sided die, the number rolled is greater than 2 with probability:
(4/6):
0.6666666666666666
or approximately 2/3 of the trials:
0.6666666666666666
Exercise 4 Part 3b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def roll_greater_than_two(num_trials):
'''Return the fraction of times that a roll of a six-sided die produces a number greater than 2.'''
count = 0
for i in range(num_trials):
if random.randrange(6)+1 > 2:
count = count + 1
print(f"Fraction of times we got a roll > 2 in {num_trials} trials: {count/num_trials}")
roll_greater_than_two(100_000)
Fraction of times we got a roll > 2 in 100000 trials: 0.6669
The simulation in (b) shows we get a roll greater than 2 in about 2/3 or about 0.67 of the large number of trials as expected.
# (4.)
# (a)
print("For n = 2 rolls of a fair six-sided die, the number rolled is greater than 2 with probability:")
print("35/36")
print("or approximately 35/36 of the trials:")
print(35/36)
For n = 2 rolls of a fair six-sided die, the number rolled is greater than 2 with probability:
35/36
or approximately 35/36 of the trials:
0.9722222222222222
Exercise 4 Part 4b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def sum_greater_than_two(num_trials):
'''Return the fraction of times that two rolls of a six-sided die produces a number greater than 2.'''
count = 0
for i in range(num_trials):
if random.randrange(6)+1 + random.randrange(6)+1 > 2:
count = count + 1
print(f"Fraction of times we get two rolls with sum > 2 in {num_trials} trials: {count/num_trials}")
sum_greater_than_two(100_000)
Fraction of times we get two rolls with sum > 2 in 100000 trials: 0.97319
The simulation in (b) shows we get a sum greater than 2 in about 0.97 of the large number of trials as expected.
# (5.)
# (a)
print("For n = 2 rolls of a fair six-sided die, the numbers rolled are different with probability:")
print("5/6")
print("or approximately 5/6 of the trials:")
print(5/6)
For n = 2 rolls of a fair six-sided die, the numbers rolled are different with probability:
5/6
or approximately 5/6 of the trials:
0.8333333333333334
Exercise 4 Part 5b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def two_different(num_trials):
'''Return the fraction of times that two rolls of a six-sided die produce two different numbers.'''
count = 0
for i in range(num_trials):
if random.randrange(6)+1 != random.randrange(6)+1:
count = count + 1
print(f"Fraction of times we get two rolls that are different from each other in {num_trials} trials of two rolls: {count/num_trials}")
two_different(100_000)
Fraction of times we get two rolls that are different from each other in 100000 trials of two rolls: 0.83389
The simulation in (b) shows that two rolls produce two different numbers about 0.83 of the large number of trials as expected.
# (6.)
# (a)
print("For n = 3 rolls of a fair six-sided die,")
print("* two numbers are the same, and one is different")
print("if")
print("* they are not all different, and they are not all the same,")
print("so we get two the same and one different with probability:")
print("1 - 1*5/6*4/6 - 1/36")
print("or approximately 1 - 20/36 - 1/36 of the trials:")
print(15/36)
For n = 3 rolls of a fair six-sided die,
* two numbers are the same, and one is different
if
* they are not all different, and they are not all the same,
so we get two the same and one different with probability:
1 - 1*5/6*4/6 - 1/36
or approximately 1 - 20/36 - 1/36 of the trials:
0.4166666666666667
Exercise 4 Part 6b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def two_same_one_different(num_trials):
'''Return the fraction of times that three rolls of a six-sided die produce two numbers the same and one different.'''
count = num_trials
rolls = []
for i in range(num_trials):
for j in range(3):
rolls.append(random.randrange(6)+1)
if rolls[0] == rolls[1] and rolls[0] == rolls[2]:
count = count - 1
elif rolls[0] != rolls[1] and rolls[1] != rolls[2] and rolls[0] != rolls[2]:
count = count - 1
rolls = []
print(f"Fraction of times that three rolls produce two numbers that are the same and one that is different in {num_trials} trials of three rolls: {count/num_trials}")
two_same_one_different(100_000)
Fraction of times that three rolls produce two numbers that are the same and one that is different in 100000 trials of three rolls: 0.41633
The simulation in (b) shows that three rolls produce two of the same numbers and one different about 0.42 of the large number of trials as expected.
# (7.)
# (a)
print("For n = 6 rolls of a fair six-sided die, the probability that all six numbers are different is:")
print("1 * 5/6 * 4/6 * 3/6 * 2/6 * 1/6")
print("or approximately 120/6**5 of the trials:")
print(120/6**5)
print("It happens approximately 1.5 times out of 100 on average:")
print(1.5/100)
For n = 6 rolls of a fair six-sided die, the probability that all six numbers are different is:
1 * 5/6 * 4/6 * 3/6 * 2/6 * 1/6
or approximately 120/6**5 of the trials:
0.015432098765432098
It happens approximately 1.5 times out of 100 on average:
0.015
Exercise 4 Part 7b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def six_rolls_all_different(num_trials):
'''Return the number of times that six rolls of a six-sided die produce all different numbers.'''
rolls = []
count = 0
for i in range (num_trials):
for j in range(6):
rolls.append(random.randrange(6)+1)
if rolls.count(1) == 1 and rolls.count(2) == 1 and rolls.count(3) == 1 and rolls.count(4) == 1 and rolls.count(5) == 1 and rolls.count(6) == 1:
count = count + 1
rolls = []
return count
def repeat_trials_different(reps):
'''Print the number of times that six rolls of a six-sided die produce all different numbers in 100 trials,
and print the average number of such sequences over reps repetitions of 100 trials.'''
count = 0
num_successes = 0
for i in range(reps):
num_successes = six_rolls_all_different(100)
print(num_successes)
count = count + num_successes
print(f"Average: {count/reps}")
print("How many times to we get all the numbers different in 100 trials when we do 100 trials ten times?")
repeat_trials_different(10)
How many times to we get all the numbers different in 100 trials when we do 100 trials ten times?
3
3
1
0
1
1
0
1
3
2
Average: 1.5
On average we get all the numbers different around 1.5 times in 100 trials as expected.
# (8.)
# (a)
print("For n = 100 rolls of a fair six-sided die, the probability that all 100 numbers are the same is:")
print("1 * (1/6)**99")
print("or approximately 1/6**99 of the trials:")
print(1/6**99)
print("It happens essentially never.")
For n = 100 rolls of a fair six-sided die, the probability that all 100 numbers are the same is:
1 * (1/6)**99
or approximately 1/6**99 of the trials:
9.183880244919038e-78
It happens essentially never.
Exercise 4 Part 8b)
Show code cell source
repeat_trials(10, 100)
0
0
0
0
0
0
0
0
0
0
Average: 0.0
# (9.)
# (a)
print("For n = 6 rolls of a fair six-sided die, the probability that the number 1 appears at least once is:")
print("1 - (5/6)**6")
print("or approximately 66.5% of the trials:")
print(1 - (5/6)**6)
For n = 6 rolls of a fair six-sided die, the probability that the number 1 appears at least once is:
1 - (5/6)**6
or approximately 66.5% of the trials:
0.6651020233196159
Exercise 4 Part 9b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def at_least_1_one(num_trials):
'''Return the fraction of times that six rolls of a six-sided die produce at least 1 one.'''
count = 0
rolls = []
for i in range(num_trials):
for j in range(6):
rolls.append(random.randrange(6)+1)
if rolls.count(1) > 0:
count = count + 1
rolls = []
print(f"Fraction of times that six rolls produce at least 1 one in {num_trials} trials of six rolls: {count/num_trials}")
at_least_1_one(100_000)
Fraction of times that six rolls produce at least 1 one in 100000 trials of six rolls: 0.66659
The simulation in (b) shows that six rolls produce at least 1 one in about 0.67 of the large number of trials as expected.
# (10.)
# (a)
print("For n = 6 rolls of a fair six-sided die, the probability that the number 1 appears at most once is:")
print("(5/6)**6 + 1/6*(5/6)**5 * 6")
print("or approximately (5/6)**6 + (5/6)**5% of the trials:")
print((5/6)**6 + (5/6)**5)
For n = 6 rolls of a fair six-sided die, the probability that the number 1 appears at most once is:
(5/6)**6 + 1/6*(5/6)**5 * 6
or approximately (5/6)**6 + (5/6)**5% of the trials:
0.7367755486968453
Exercise 4 Part 10b)
Show code cell source
# (b) Computationally, we can proceed as follows:
def at_most_1_one(num_trials):
'''Return the fraction of times that six rolls of a six-sided die produce at most 1 one.'''
count = 0
rolls = []
for i in range(num_trials):
for j in range(6):
rolls.append(random.randrange(6)+1)
if rolls.count(1) < 2:
count = count + 1
rolls = []
print(f"Fraction of times that six rolls produce at most 1 one in {num_trials} trials of six rolls: {count/num_trials}")
at_most_1_one(100_000)
Fraction of times that six rolls produce at most 1 one in 100000 trials of six rolls: 0.73633
The simulation in (b) shows that six rolls produce 0 or 1 one in about 0.7 of the large number of trials as expected.
Exercise 5: Consider the function below. Add comments to explain the code. Summarize the purpose of the function in a complete sentence. Demonstrate its performance on a sample run. Summarize the results in a complete sentence.
Show code cell source
def flip(num_flips):
'''Return the fraction of heads in num_flips coin flips.'''
head_count = 0
# Do num_flips coin flips.
for i in range(num_flips):
# If the flip is heads, increment heads counter.
if random.choice(('H', 'T')) == 'H':
head_count += 1
# Return the fraction of heads flipped.
return head_count/num_flips
print(flip(10_000))
0.5027
The sample run does 10,000 flips. The function returns the fraction of heads, which came out to 0.4966 on one run and to 0.5027 on another.
Exercise 6: Consider the function below. Add comments to explain the code. Summarize the purpose of the function in a complete sentence. Demonstrate its performance on a sample run. Summarize the results in a complete sentence.
Show code cell source
def flip_trials_preliminary(num_flips_per_trial, num_trials):
'''Flips a coin num_flips_per_trial times, calculates the fraction of heads,
and repeats for num_trials trials. Returns the average of all num_trials fractions.'''
fraction_heads = []
for i in range(num_trials): # In each trial
# Call the function flip defined above.
# Append the fraction of heads in num_flips_per_trial coin flips into the list.
fraction_heads.append(flip(num_flips_per_trial))
mean = sum(fraction_heads) / len(fraction_heads)
return mean
print(flip_trials_preliminary(100, 1000))
0.5029899999999993
The sample run does 1000 trials (in which 100 coin flips are executed and the fraction of heads is computed). The function returns the average of the 1000 fractions of heads, which came out to 0.49915999999999944 on one run and to 0.5029899999999993 on another.
Exercise 7. When a fair coin is flipped once, the theoretical probability that the outcome will be heads is equal to 1/2. Therefore, according to the LLN, the proportion of heads in a “large” number \(n\) of coin flips “should be” roughly 1⁄2, and the proportion of heads approaches 1/2 as \(n\) approaches infinity. Illustrate this idea using simulation with a larger and larger number of flips.
print(flip(10))
print(flip(100))
print(flip(1000))
print(flip(10_000))
0.3
0.54
0.495
0.5039
When I flip 10, 100, 1000, and 10,000 times, respectively, I get fractions of heads, for example, 0.3, 0.54, 0.495, 0.5039, respectively.
5.9.3. Conditional probability#
Exercise 1: Suppose 35 spam email messages contain the word “free”; 25 spam messages do not contain the word “free”; three of non-spam messages contain the word “free”; and 37 non-spam messages do not contain the word “free”. (This problem is adapted from OpenIntoStatistics, David M. Diez, Christoper D. Barr, and Mine Cetinkaya-Rundel, Creative Commons, 2016.)
Do the following problems and interpret your answer in complete sentences.
(a) Calculate the probability that a message is spam, given that it contains the word “free”.
(b) Calculate the probability that a message is not spam, given that it contains the word “free”.
(c) Calculate the probability that a message contains the word “free”, given that it is spam.
(d) Verify that Bayes’ Theorem holds for some data from this problem.
(e) Which of the above quantities do you consider to be of the most practical interest?
(f) Suppose we are trying to make decisions about whether a message is spam. Calculate the most relevant probabilities, explain their significance in the context of the practical problem at hand, and describe possible limitations of their applicability.
Exercise 1a)
Show code cell source
# F: Email contains the word "free".
# NF: Email does not contain the word "free".
# S: Email is spam.
# NS: Email is not spam.
# There are 100 emails.
# (a)
# P(S|F) = P(S and F)/P(F)
35/100 / ((35 + 3)/100)
# The probability that a message is spam, given that it contains the word "free" is:
0.9210526315789473
Exercise 1b)
Show code cell source
# (b)
# P(NS | F) = P(NS and F)/P(F)
3/100 / (38/100)
# The probability that a message is not spam, given that it contains the word "free" is:
0.07894736842105263
Exercise 1c)
Show code cell source
# (c)
# P (F | S) = P(F and S)/P(S)
pFgS = 35/100 / ((35 + 25)/100)
print(pFgS)
# The probability that a message contains the word "free", given that it is spam is:
0.5833333333333334
Exercise 1d)
# (d)
# According to Bayes' Theorem, P(S | F) = P(F | S) P(S) / P(F) or:
pFgS * 60/100 / (38/100)
# which agrees with (a).
0.9210526315789473
Exercise 1e)
Probably the most practical number is the probability of spam, given the email contains the word “free” because checking for spam is something you might want to do. It seems that “free” comes up a lot in spam messages. It may be a useful marker because the probability of spam given the possibly related word “free” is about 92%. One limitation of this conclusion is that it is based only on the data provided. We would need reasons to believe that the data are representative of all emails, spam and not spam, that do and do not contain the word “free”. Also practically all spam messages contain the word “the”, so we have to be confident that “free” is not so widespread that it isn’t helpful. Here the probability that a message is not spam, given that it has the word “free” is somewhat small: about 8%.
Exercise 2: Suppose the disease meningitis causes a stiff neck 70% of the time, the prior probability of any patient having meningitis is 1/50,000, and the prior probability of any patient having a stiff neck is 1/100. (Artificial Intelligence: A Modern Approach (Third Edition), Stuart J. Russell and Peter Norvig, Prentice Hall, Upper Saddle River, 2010). Use Bayes’ Theorem to calculate the probability that a patient has meningitis, given they have a stiff neck. Show how you apply Bayes’ Theorem. Interpret the results in a complete sentence.
Show code cell source
# The probability of M (a patient having meningitis), given S (they have a stiff neck) is
# P(M | S) = P(S | M) P(M) / P(S) or
0.7 * 1/50_000 / (1/100)
# or 1.4 in 1000.
0.0014
5.9.4. Probability Distributions#
Exercise 1: Consider points \((x, y)\) in a 1 x 1 square in the first quadrant of the plane \((x, y) \in [0, 1) \times [0, 1)\). Simulate filling the square with dots by picking points in the square at random. Generate the coordinates in each \(x\)-\(y\) pair by using Python to sample from a uniform distribution on the interval [0, 1). Use the ratio of number of dots inside a quarter circle with center at the origin to total dots to simulate the ratio of the area of the quarter circle to the area of the square. Use this ratio to to estimate the value of \(\pi\).
Show code cell source
total_points = 100_000
circle_points = 0
for i in range(total_points):
x, y = random.uniform(-1, 1), random.uniform(-1, 1)
if x**2 + y**2 < 1:
circle_points = circle_points + 1
print(4 * circle_points/total_points)
3.14152
Exercise 2: 1. Use Python to simulate a game board in which 10,000 balls are dropped down onto a triangle of ten levels of pegs, one-by-one. Level 1 has 1 peg. Level 2 below it has 2 pegs, etc., down to 10 pegs at Level 10 at the bottom. Assume each ball has equal probability of moving to the left or to the right at each level.
(a) Plot the number of balls against the landing-peg number. Include a descriptive title and labels for both axes on your plot.
(b) How does the graph tend to change if you use more levels and keep the number of balls the same? Why?
(c) How does the graph tend to change if you use more balls and keep the number of levels the same? Why?
Show code cell source
import numpy as np
import matplotlib
def board_game(balls, levels):
# The number levels is the number of levels (excluding 0th level) and number of pegs at bottom level
total_balls = np.zeros(levels) # array to keep a record of how many balls land in each position
for i in range(balls): # For each trial:
current_position = 0
for level in range(1, levels): # Start at Level 1 and go up to and not including the bottom row.
current_position += random.randrange(2) # Increment the current position by 0 (left move) or 1 (right move).
# When you're done with all levels, increment the ball total at the position where the ball ended up.
total_balls[current_position] += 1
matplotlib.pyplot.plot(total_balls)
matplotlib.pyplot.title(f"{balls} balls in a {levels}-level board with a left-bounce probability of {0.5}")
matplotlib.pyplot.xlabel('Position')
matplotlib.pyplot.ylabel('Number of balls')
matplotlib.pyplot.show()
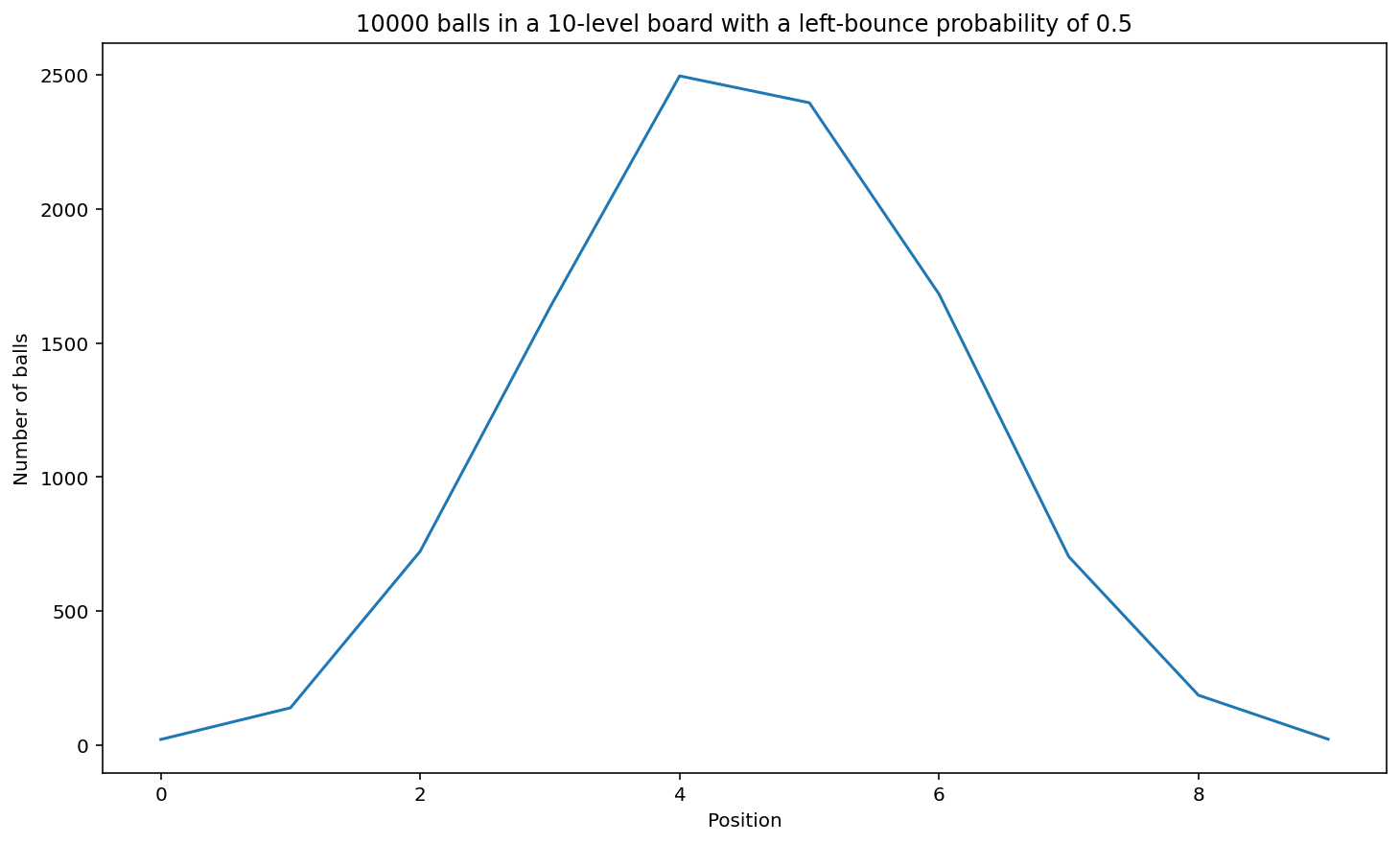
board_game(10_000, 10)
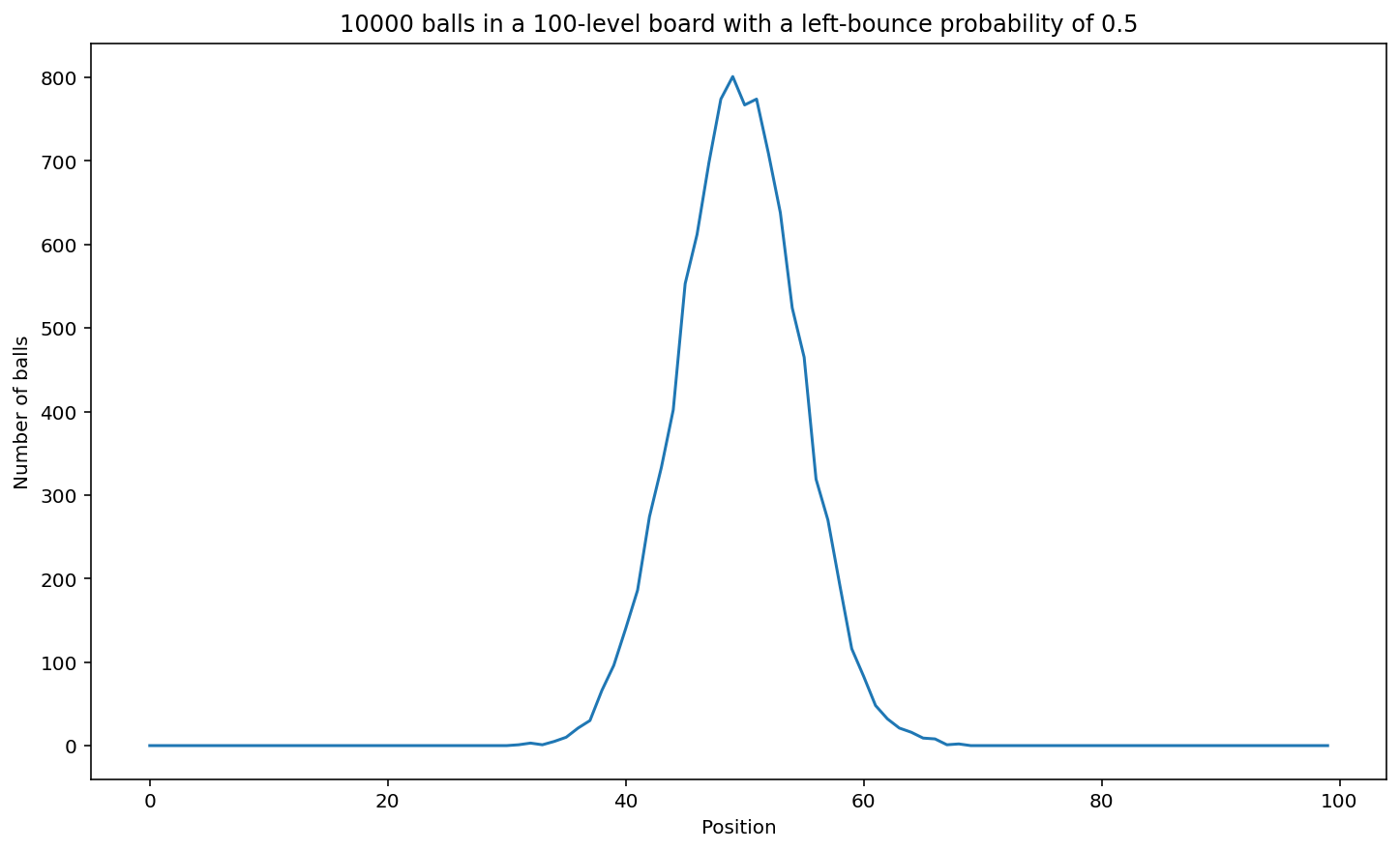
# If you use more levels and keep the number of balls the same, then the graph is very thin in the tails because it is unlikely for a ball to bounch all the way to the left or all the way to the right so many times, and the balls pile up sharply in the range of "middle" positions.
board_game(10_000, 100)
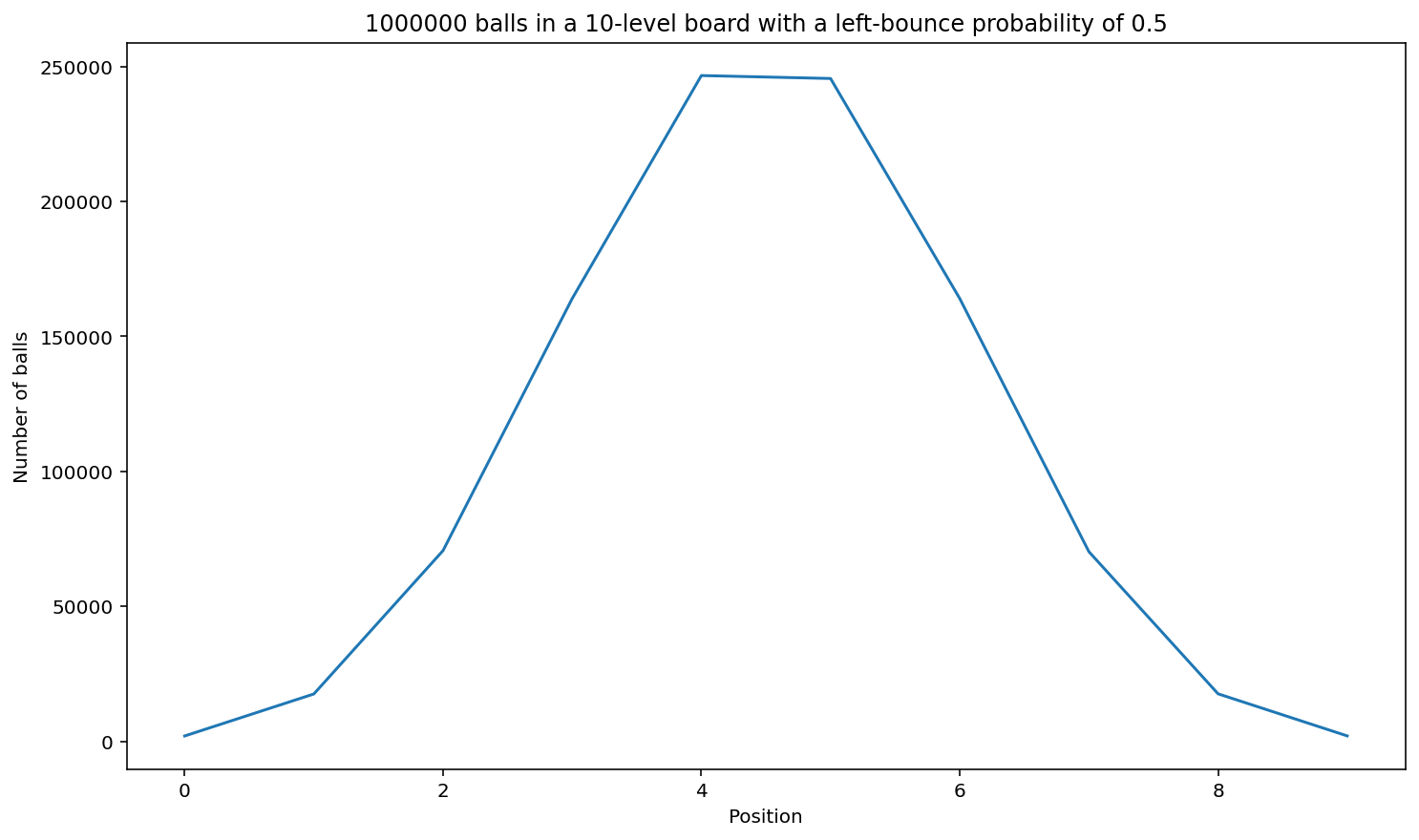
# Similarly, if you increase the number of balls and keep the the number of levels at 10, the tails are a little chunkier than before:
board_game(1_000_000, 10)
Exercise 3: Consider a biased coin that lands on heads 20% of the time. Simulate 30 flips of the coin. Record whether no heads were flipped, 1 head was flipped, 2 heads were flipped, 3 heads were flipped, etc., up to 30 heads. Repeat the experiment 10,000 times. Draw a histogram that shows how often each number 1-30 of heads was flipped. Describe the shape and spread of the graph. Compare it to the graph of the mathematical distribution given by the formula.
Show code cell source
import matplotlib.pyplot as plt
def flip_biased(p, num_flips):
'''Return the number of heads in num_flips flips of a coin
that lands on heads with probability p.'''
head_count = 0
# Do num_flips coin flips.
for i in range(num_flips):
# If the flip is heads, increment heads counter.
if random.uniform(0, 1) < p:
head_count += 1
# Return the number of heads flipped.
return head_count
def histogram_biased_coin(p, num_flips_per_trial, num_trials):
'''Make a histogram of the number of successes (heads) flipped in each of
num_trials trials, given that each flip has probability p of landing on heads.'''
successes = []
for i in range(num_trials):
successes.append(flip_biased(p, num_flips_per_trial))
'''Make a histogram that shows how many times each number 1 through num_flips_per_trial of heads
was flipped across all the num_trials trials.'''
plt.title(f'Number of successes (heads) in {num_trials} trials of {num_flips_per_trial} flips if P(heads) is {p}')
plt.xlabel('Number of heads')
plt.ylabel('Number of trials')
plt.hist(successes, bins = range(1, num_flips_per_trial), rwidth = 0.8)
xmin, xmax = 0, num_flips_per_trial
plt.figure()
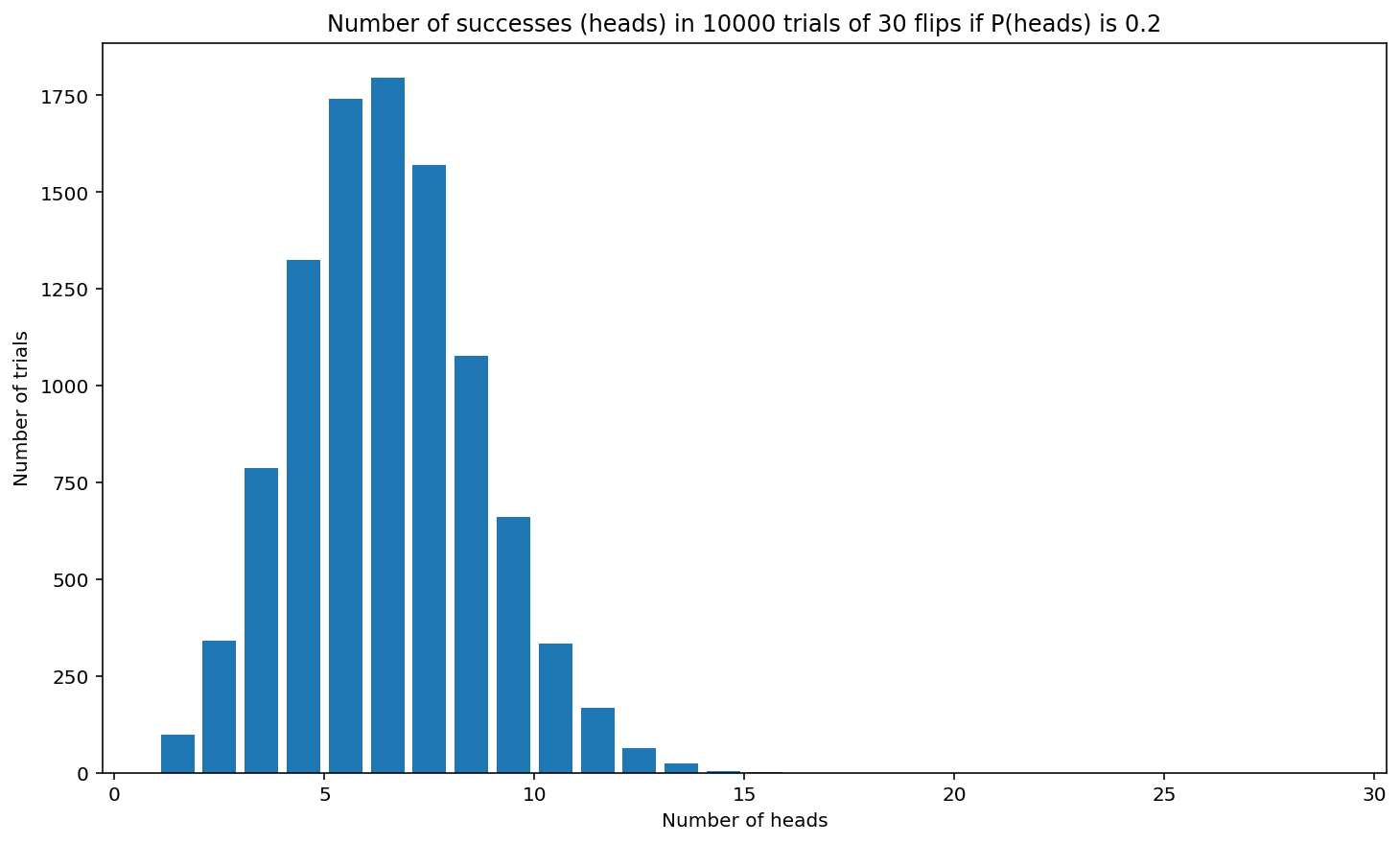
histogram_biased_coin(0.2, 30, 10_000)
This histogram shows how often each number 1-30 of heads was flipped. The most common number of heads appears to be around 5 or 6. It is very rare for this biased coin to land on heads for more than about 16 of 30 flips, so the heights of the bars are not visible for the number of heads between about 16 and 30. The graph has the shape of a binomial distribution with a shape very similar to the graph of the mathematical distribution given by the formula.
5.9.5. Random walks#
Exercise 1: A person walks on a street with an equal probability of movement to the left or right at each pace. Write a Python program to approximate the expected number of paces the person should take in order to move one pace to the left of the starting point. Suggestion: Use 0 as the starting point. State your conclusions in a complete sentence.
Show code cell source
def random_walk(probability_left, max_steps):
'''Do a random walk with probability_left probability of moving to the left on the number line and 1-probability_left of moving to the right. Start from 0. Return whether the walk arrived at position -1 within max_steps steps, and if it did, return how many steps were needed.'''
position = 0 # Start from 0.
steps = 0 # Initialize the number of steps.
# Execute the random walk.
while (position != -1) and (steps < max_steps):
r = random.uniform(0, 1) # Generate 0 <= r < 1.
if (r < probability_left):
position = position - 1 # Move left.
else:
position = position + 1 # Move right.
steps += 1
if (position == -1): # If target position was reached:
return steps
else:
return 0 # Target position was not reached.
def histogram_random_walk(num_trials, probability_left, max_steps):
'''Make a histogram of the number of steps required to reach position -1 from 0 in num_trials trials,
given that the probability of moving left at each step is probability_left. Print the number of times
that -1 was not reached within max_steps steps.'''
successes = []
failure_count = 0
for i in range(num_trials):
steps = random_walk(0.5, 100)
if steps > 0: # If target position was reached:
successes.append(steps)
else:
failure_count += 1
plt.title(f'Number of steps in {num_trials} trials required to get from 0 to -1 in a random walk of at most {max_steps} steps if the probability of moving left is {probability_left}')
plt.xlabel('Number of steps')
plt.ylabel('Number of trials')
plt.hist(successes, bins = range(1, max_steps), rwidth = 0.8)
# xmin, xmax = 0, num_flips_per_trial
plt.figure()
print(sorted(successes))
print(f"\nIn {failure_count} of {num_trials} trials ({failure_count/num_trials*100}%), the position -1 was not reached after {max_steps} steps.\n")
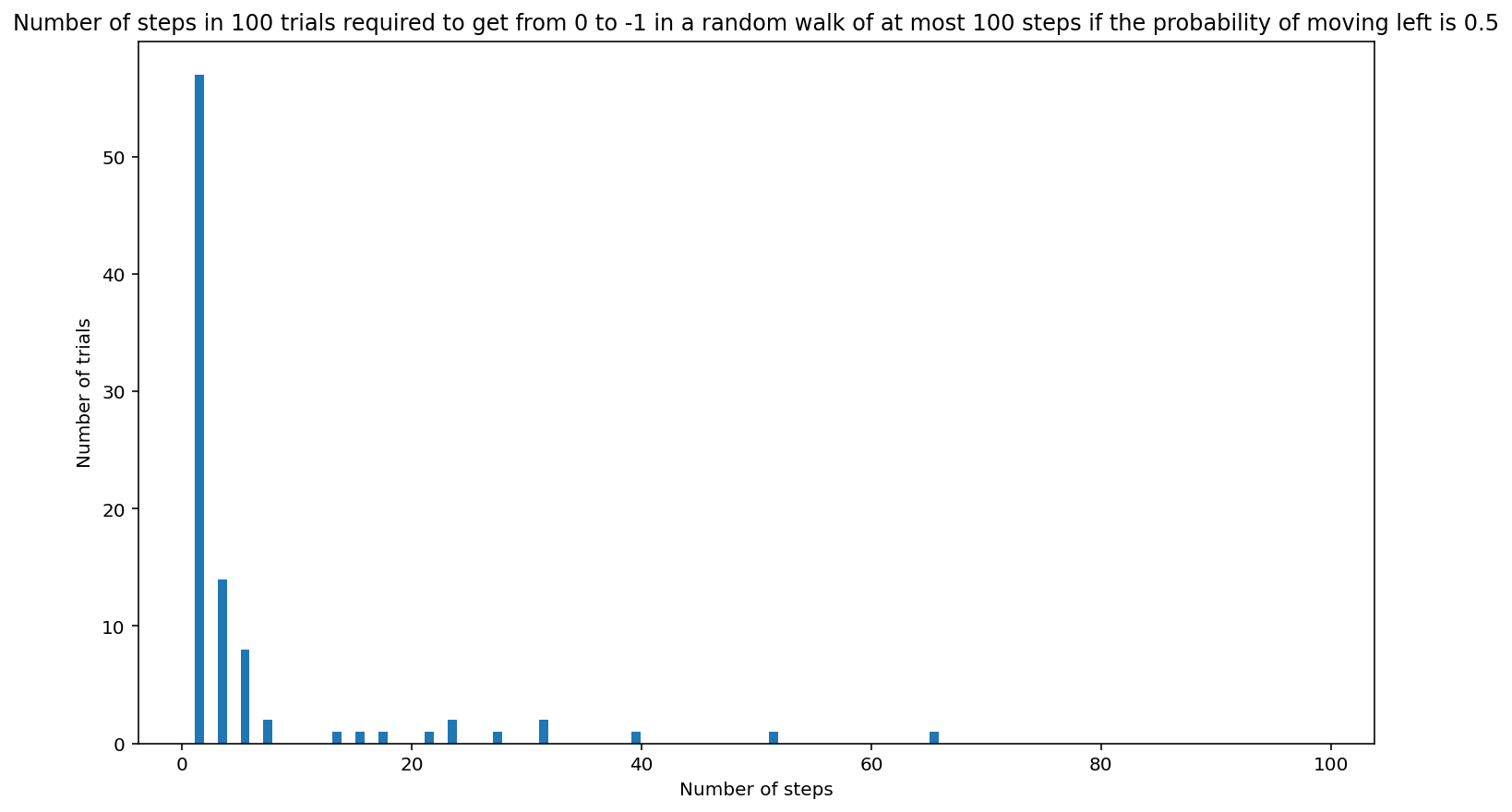
histogram_random_walk(100, 0.5, 100)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 5, 7, 7, 13, 15, 17, 21, 23, 23, 27, 31, 31, 39, 51, 65]
In 7 of 100 trials (7.000000000000001%), the position -1 was not reached after 100 steps.
<Figure size 864x504 with 0 Axes>
About half the time, it takes a person one step move one pace to the left of the starting point. This is because there is a probability of 0.5 of moving left initially (and at each step). Note that it always takes an odd number of steps to get to -1. Approximately 15% of the time, it takes three steps to get to -1. About half again as often it takes five steps. Occasionally it takes more, with path lengths 7, 9, 11, …, 99 if 100 is the maximum number of steps allowed. A small percent of the time, position -1 is not reached within 100 steps. It is not very meaningful to say what the expected number of steps is in general because the number of steps can be quite large occasionally, but we can say that about half the time we arrive at -1 in one step.
Exercise 2: Consider an unbiased random walk on a square lattice. Write a Python program to find approximate answers to the following questions:
(a) What is the expected number of a paces the person should take in order to visit the location one pace to the left of the starting point (0, 0)? Explain.
(b) How far away from the starting point (0,0) does a person end up after \(n\) steps of an unbiased random walk on a square lattice? Explain.
(c) If you run the simulation program for Part (b) many times, is there any statistical distribution you can expect? Explain.
Show code cell source
def random_walk_2d(prob_left, prob_right, prob_forward, prob_back, max_steps):
'''Do a random walk on a square lattice with equal probability of moving left, right, forward, and back. Start from (0, 0). If the walk arrived at position (-1, 0) within max_steps steps, return how many steps were needed. Otherwise return 0.'''
steps = 0 # Initialize the number of steps.
x, y = np.zeros(max_steps + 1), np.zeros(max_steps + 1)
i = 1 # Start the indexing from i-1 = 0.
# Execute the random walk.
while (not(x[i-1] == -1 and y[i-1]==0)) and (steps < max_steps):
r = random.uniform(0, 1) # Generate 0 <= r < 1.
if r < prob_forward:
x[i] = x[i-1]
y[i] = y[i-1] + 1 # Move forward.
elif r < prob_forward + prob_back:
x[i] = x[i-1]
y[i] = y[i-1] - 1 # Move back.
elif r < prob_forward + prob_back + prob_left:
x[i] = x[i-1] - 1 # Move left.
y[i] = y[i-1]
else:
x[i] = x[i-1] + 1 # Move right.
y[i] = y[i-1]
steps += 1
i += 1
if prob_left + prob_right + prob_forward + prob_back != 1:
print ("ERROR: Probabilities must sum to 1.")
if (x[i-1] == -1 and y[i-1] == 0): # If target position was reached:
return steps
else:
return 0 # Target position was not reached.
def histogram_random_walk_2d(prob_left, prob_right, prob_forward, prob_back, num_trials, max_steps):
'''Make a histogram of the number of steps required to reach position (-1, 0) in num_trials trials
starting from (0, 0) in an unbiased random walk on a square lattice. Print the number of times
that (-1, 0) was not reached within max_steps steps.'''
successes = []
failure_count = 0
for i in range(num_trials):
steps = random_walk_2d(prob_left, prob_right, prob_forward, prob_back, 100)
if steps > 0: # If target position was reached:
successes.append(steps)
else:
failure_count += 1
plt.title(f'Number of steps in {num_trials} trials required to get from (0, 0) to (-1, 0) in a random walk of at most {max_steps} steps in an unbiased random walk on a square lattice')
plt.xlabel('Number of steps')
plt.ylabel('Number of trials')
plt.hist(successes, bins = range(1, 100), rwidth = 0.8)
plt.figure()
print(sorted(successes))
print(f"\nIn {failure_count} of {num_trials} trials ({failure_count/num_trials*100}%), the position (-1, 0) was not reached after {max_steps} steps.\n")
print(f"The person arrived at (-1, 0) in three steps {successes.count(3)} times.")
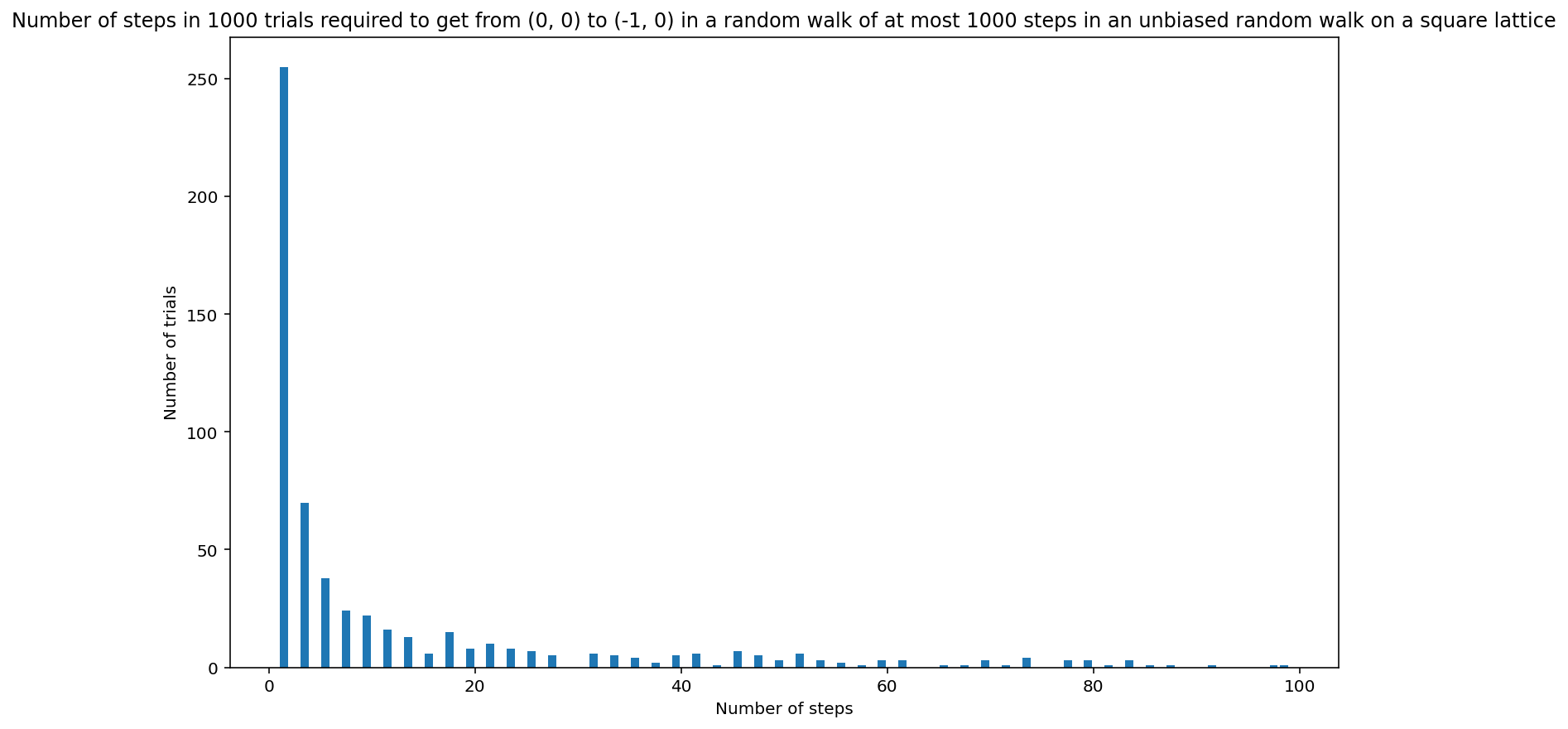
histogram_random_walk_2d(0.25, 0.25, 0.25, 0.25, 1000, 1000)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 15, 15, 15, 15, 15, 15, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 19, 19, 19, 19, 19, 19, 19, 19, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 23, 23, 23, 23, 23, 23, 23, 23, 25, 25, 25, 25, 25, 25, 25, 27, 27, 27, 27, 27, 31, 31, 31, 31, 31, 31, 33, 33, 33, 33, 33, 35, 35, 35, 35, 37, 37, 39, 39, 39, 39, 39, 41, 41, 41, 41, 41, 41, 43, 45, 45, 45, 45, 45, 45, 45, 47, 47, 47, 47, 47, 49, 49, 49, 51, 51, 51, 51, 51, 51, 53, 53, 53, 55, 55, 57, 59, 59, 59, 61, 61, 61, 65, 67, 69, 69, 69, 71, 73, 73, 73, 73, 77, 77, 77, 79, 79, 79, 81, 83, 83, 83, 85, 87, 91, 97, 99]
In 416 of 1000 trials (41.6%), the position (-1, 0) was not reached after 1000 steps.
The person arrived at (-1, 0) in three steps 70 times.
<Figure size 864x504 with 0 Axes>
(a) About 25% of the time, it takes a person one step to move one pace to the left of the starting point. This is because there is a probability of 0.25 of moving left initially (and at each step). Note that it always takes an odd number of steps to get to (-1, 0). Approximately 7.5% of the time, it takes three steps to get to (-1, 0). About half again as often it takes five steps. Occasionally it takes more, with path lengths 7, 9, 11, …, 999, if 1000 is the maximum number of steps allowed. About 40% of the time, position (-1, 0) is not reached within 1000 steps. It is not very meaningful to say what the expected number of steps is in general because the number of steps can vary a lot, can be very large, and most commonly takes the person so far from (-1, 0) that our simulation gives up on having them return. However, we can say that about 25% of the time we arrive at (-1, 0) in one step.
Show code cell source
def how_far(num_forward, num_back, num_left, num_right, num_trials, num_steps):
'''Make a histogram of the distances reached from the origin in num_trials trials
of a random walk of n unbiased steps on a square lattice.
We assume that the probability of going forward, back, left, and right is the same.
When the walk goes forward, it goes forward num_forward steps.
When the walk goes back, it goes forward num_back steps.
When the walk goes left, it goes left num_left steps.
When the walk goes right, it goes forward num_right steps.'''
n = num_steps # Use parameter name from problem statement.
distances = []
for trials in range(1, num_trials):
# Use the code from the chapter in the body of the loop.
x, y = np.zeros(n), np.zeros(n)
for i in range(1, n):
val = random.choice(['forward', 'back', 'left', 'right'])
if val == 'forward':
x[i] = x[i-1]
y[i] = y[i-1] + num_forward
elif val == 'back':
x[i] = x[i-1]
y[i] = y[i-1] - num_back
elif val == 'left':
x[i] = x[i-1] - num_left
y[i] = y[i-1]
else: # val == 'right'
x[i] = x[i-1] + num_right
y[i] = y[i-1]
distances.append(abs(x[n-1]) + abs(y[n-1]))
plt.title(f'Distance reached from the origin in {num_trials} trials of a random walk of {n} unbiased steps on a square lattice.')
plt.xlabel('Distance from the origin')
plt.ylabel('Number of trials')
plt.hist(distances, bins = range(1, int(max(distances))), rwidth = 0.8)
plt.figure()
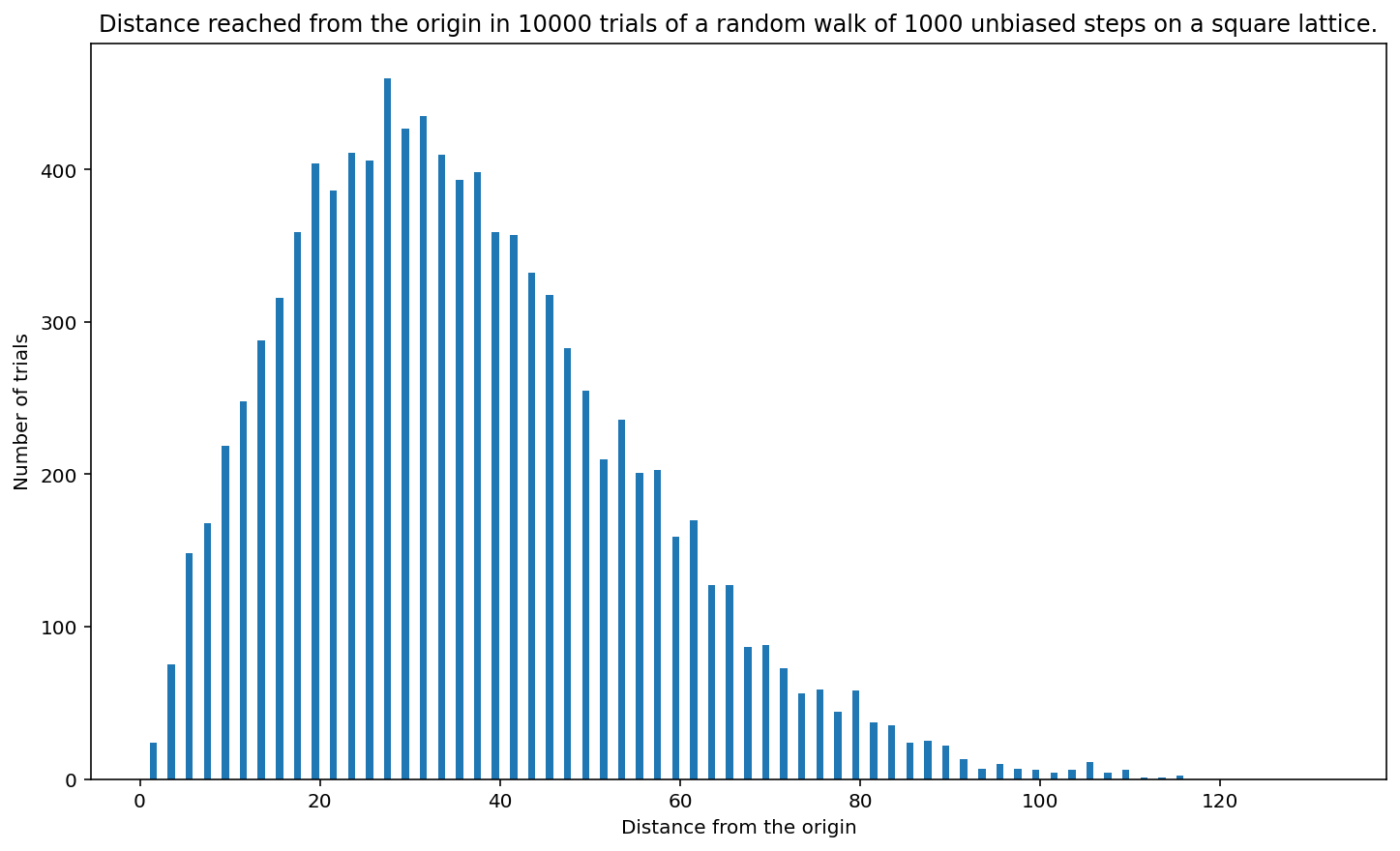
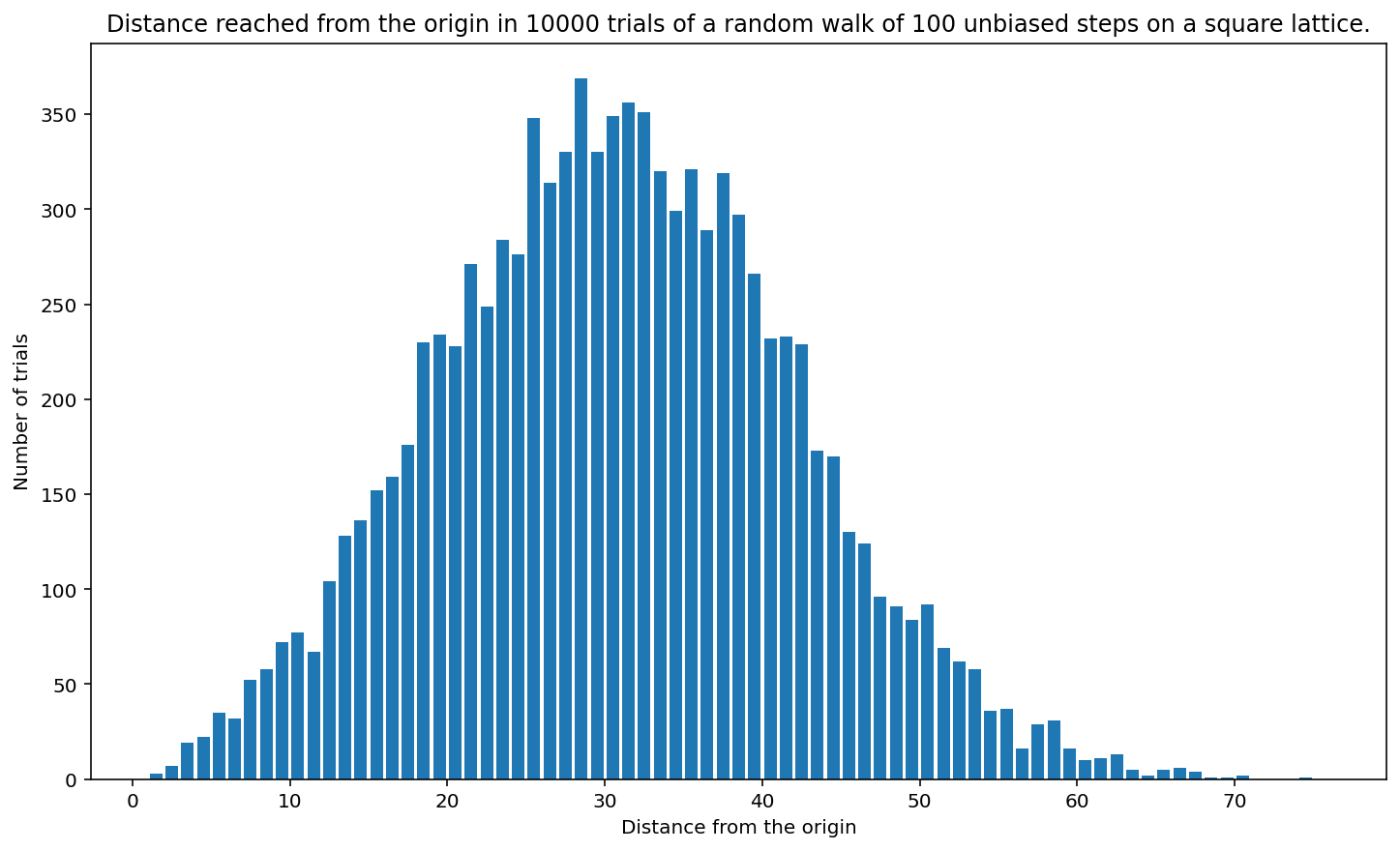
how_far(1, 1, 1, 1, 10_000, 1000)
(b) If a person ends up at position \((x, y)\), we can consider them to be a distance \(|x| + |y|\) from the origin. In \(100\) steps, a person most commonly ends up about 10 “city blocks” from the origin. In 1000 steps, a person most commonly ends up about 30 units from the origin. (It can be shown mathematically that the distance the person ends up from the origin is proportional to \(\sqrt{n}\) for long walks of \(n\) steps.)
(c) The distribution of distances looks like a binomial distribution as shown.
Exercise 3: A person walks one pace left with a probability of 0.35, one pace right with a probability of 0.2, one pace forward with a probability of 0.4 and one pace backward with a probability of 0.05. Write a Python program to approximate the expected number of paces the person should take in order to visit the location one pace to the left of the starting point. State your conclusions in a complete sentence.
Show code cell source
histogram_random_walk_2d(0.35, 0.2, 0.4, 0.05, 1000, 1000)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 9, 9, 9, 9, 11]
In 544 of 1000 trials (54.400000000000006%), the position (-1, 0) was not reached after 1000 steps.

<Figure size 864x504 with 0 Axes>
About 35% of the time, it takes a person one step to move one pace to the left of the starting point. This is because there is a probability of 0.35 of moving left initially (and at each step). Note that it always takes an odd number of steps to get to (-1, 0). Approximately 5% of the time, it takes three steps to get to (-1, 0). About half again as often it takes five steps. Occasionally it takes more, with path lengths slightly longer like 7, 9, or 11. About 50% of the time, position (-1, 0) is not reached within 1000 steps. It looks like if the person doesn’t reach (-1, 0) within a relatively small number of steps like 11, then they do not reach the position at all withing 1000 steps. It is not very meaningful to say what the expected number of steps is in general because the arrival time is typically either in one step or (for all practical purposes) never. We can certainly say that about 35% of the time we arrive at (-1, 0) in one step.
Exercise 4: A person walks one pace left, right, forward or back with equal probability. When the person walks left, right, or back, she walks one pace. When she walks forward, she walks two paces. Write a Python program to approximate how far forward the person has walked in 1000 paces. State your conclusions in a complete sentence.
Show code cell source
def how_far_forward(num_forward, num_back, num_left, num_right, num_trials, num_steps):
'''Make a histogram of how far forward a person goes in num_trials trials
of a random walk of n unbiased steps on a square lattice.
We assume that the probability of going forward, back, left, and right is the same.
When the walk goes forward, it goes forward num_forward steps.
When the walk goes back, it goes forward num_back steps.
When the walk goes left, it goes left num_left steps.
When the walk goes right, it goes forward num_right steps.'''
n = num_steps # Use parameter name from problem statement.
distances_forward = []
for trials in range(1, num_trials):
# Use the code from the chapter in the body of the loop.
x, y = np.zeros(n), np.zeros(n)
for i in range(1, n):
val = random.choice(['forward', 'back', 'left', 'right'])
if val == 'forward':
x[i] = x[i-1]
y[i] = y[i-1] + num_forward
elif val == 'back':
x[i] = x[i-1]
y[i] = y[i-1] - num_back
elif val == 'left':
x[i] = x[i-1] - num_left
y[i] = y[i-1]
else: # val == 'right'
x[i] = x[i-1] + num_right
y[i] = y[i-1]
distances_forward.append(x[n-1])
plt.title(f'Distance reached from the origin in {num_trials} trials of a random walk of {n} unbiased steps on a square lattice.')
plt.xlabel('Distance forward from 0')
plt.ylabel('Number of trials')
plt.hist(distances_forward, bins = range(1, int(max(distances_forward))), rwidth = 0.8)
plt.figure()
how_far(2, 1, 1, 1, 10_000, 100)
If a person ends up at position \((x, y)\), we can consider them to be \(x\) units forward of the starting position (0, 0). In \(100\) steps, a person most commonly ends up about 27 units forward. In 1000 steps, a person most commonly ends up about 270 units forward. A histogram of distances forward has its peak skewed left as shown.
Exercise 5: A Markov chain describes a sequence of possible events in which the probability of each event depends on the state in the previous event. For example, suppose that we modify an unbiased random walk on a square lattice such that if the previous step was to the right, then the probability of making the current move up, down, left, or right is 0.2, 0.2, 0.4, or 0.2, respectively. As such,
(a) explain the implications of a move to the right in practical terms in a complete sentence.
(b) run some simulations and address the question: How does the use of the Markov chain change the unbiased random walk on a square lattice?
(a) In this problem, a move to the right makes the walker more likely to go left directly afterward.
Show code cell source
def random_walk_markov(prob_left, prob_right, prob_forward, prob_back, max_steps):
'''Do a random walk on a square lattice with equal probability of moving left, right, forward, and back.
Start from (0, 0).
If the step is to the right, then the probability of making the next move up, down, left, or right is
0.2, 0.2, 0.4, or 0.2, respectively.
If the walk arrived at position (-1, 0) within max_steps steps, return how many steps were needed.
Otherwise return 0.'''
steps = 0 # Initialize the number of steps.
step_right = False
x, y = np.zeros(max_steps + 1), np.zeros(max_steps + 1)
i = 1 # Start the indexing from i-1 = 0.
# Execute the random walk.
while (not(x[i-1] == -1 and y[i-1]==0)) and (steps < max_steps):
r = random.uniform(0, 1) # Generate 0 <= r < 1.
if not(step_right): # If the previous move was not to the right:
if r < prob_forward:
x[i] = x[i-1]
y[i] = y[i-1] + 1 # Move forward.
elif r < prob_forward + prob_back:
x[i] = x[i-1]
y[i] = y[i-1] - 1 # Move back.
elif r < prob_forward + prob_back + prob_left:
x[i] = x[i-1] - 1 # Move left.
y[i] = y[i-1]
else:
x[i] = x[i-1] + 1 # Move right.
y[i] = y[i-1]
step_right = True
else: # The previous step was to the right, so:
# Make the next move forward, back, left, or right with probability 0.2, 0.2, 0.4, or 0.2, respectively.
r = random.uniform(0, 1) # Generate 0 <= r < 1.
if r < 0.2:
x[i] = x[i-1]
y[i] = y[i-1] + 1 # Move forward.
step_right = False
elif r < 0.4:
x[i] = x[i-1]
y[i] = y[i-1] - 1 # Move back.
step_right = False
elif r < 0.8:
x[i] = x[i-1] - 1 # Move left.
y[i] = y[i-1]
step_right = False
else:
x[i] = x[i-1] + 1 # Move right.
y[i] = y[i-1]
steps += 1
i += 1
if prob_left + prob_right + prob_forward + prob_back != 1:
print ("ERROR: Probabilities must sum to 1.")
if (x[i-1] == -1 and y[i-1] == 0): # If target position was reached:
return steps
else:
return 0 # Target position was not reached.
def histogram_random_walk_markov(prob_left, prob_right, prob_forward, prob_back, num_trials, max_steps):
'''Make a histogram of the number of steps required to reach position (-1, 0) in num_trials trials
starting from (0, 0) in an unbiased random walk on a square lattice. Print the number of times
that (-1, 0) was not reached within max_steps steps.'''
successes = []
failure_count = 0
for i in range(num_trials):
steps = random_walk_markov(prob_left, prob_right, prob_forward, prob_back, 100)
if steps > 0: # If target position was reached:
successes.append(steps)
else:
failure_count += 1
plt.title(f'Number of steps in {num_trials} trials required to get from (0, 0) to (-1, 0) in a random walk of at most {max_steps} steps in the Markov chain')
plt.xlabel('Number of steps')
plt.ylabel('Number of trials')
plt.hist(successes, bins = range(1, 100), rwidth = 0.8)
plt.figure()
print(sorted(successes))
print(f"\nIn {failure_count} of {num_trials} trials ({failure_count/num_trials*100}%), the position (-1, 0) was not reached after {max_steps} steps.\n")
print(f"The person arrived at (-1, 0) in three steps {successes.count(3)} times.")
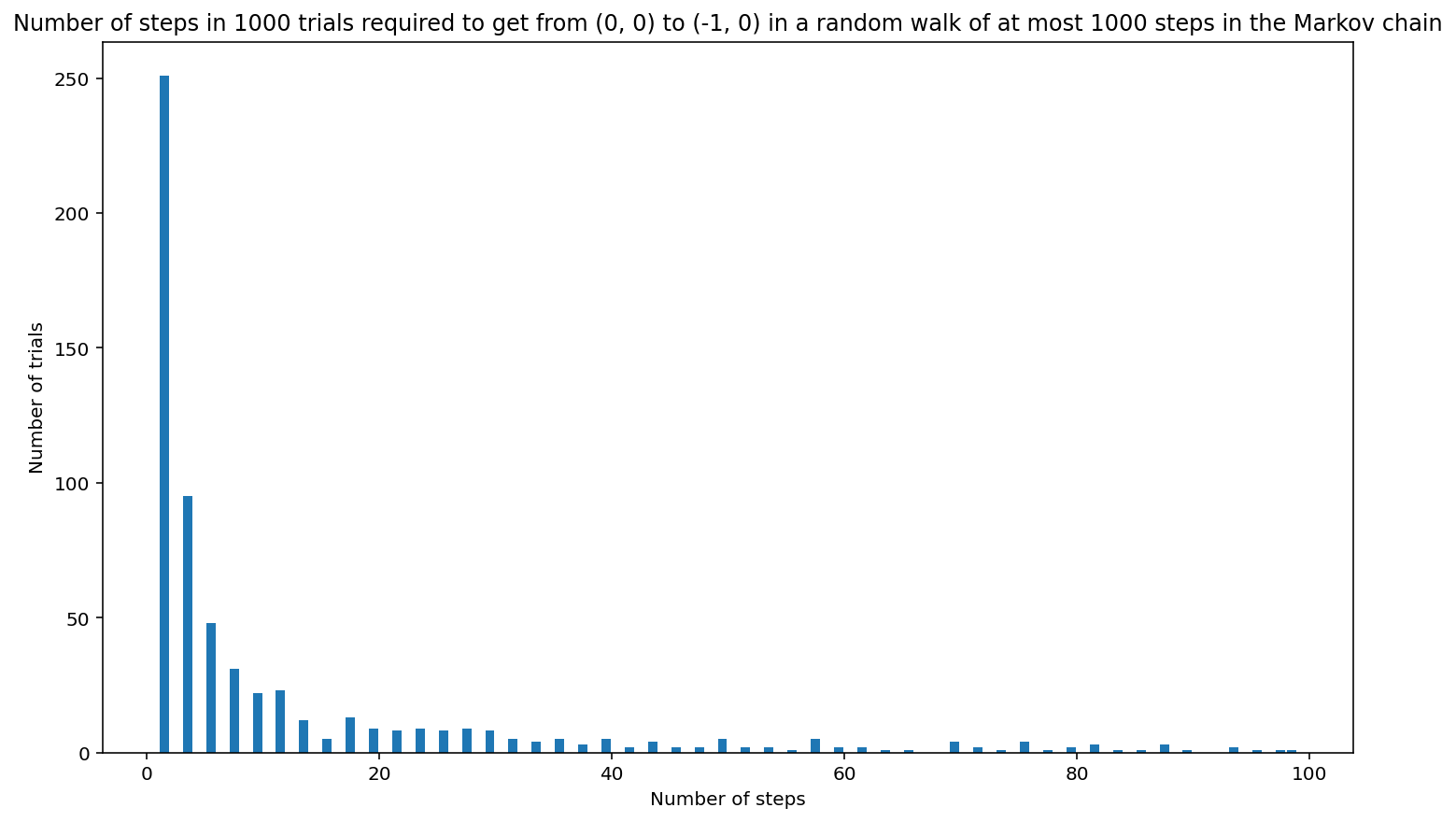
histogram_random_walk_markov(0.25, 0.25, 0.25, 0.25, 1000, 1000)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 15, 15, 15, 15, 15, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 19, 19, 19, 19, 19, 19, 19, 19, 19, 21, 21, 21, 21, 21, 21, 21, 21, 23, 23, 23, 23, 23, 23, 23, 23, 23, 25, 25, 25, 25, 25, 25, 25, 25, 27, 27, 27, 27, 27, 27, 27, 27, 27, 29, 29, 29, 29, 29, 29, 29, 29, 31, 31, 31, 31, 31, 33, 33, 33, 33, 35, 35, 35, 35, 35, 37, 37, 37, 39, 39, 39, 39, 39, 41, 41, 43, 43, 43, 43, 45, 45, 47, 47, 49, 49, 49, 49, 49, 51, 51, 53, 53, 55, 57, 57, 57, 57, 57, 59, 59, 61, 61, 63, 65, 69, 69, 69, 69, 71, 71, 73, 75, 75, 75, 75, 77, 79, 79, 81, 81, 81, 83, 85, 87, 87, 87, 89, 93, 93, 95, 97, 99]
In 368 of 1000 trials (36.8%), the position (-1, 0) was not reached after 1000 steps.
The person arrived at (-1, 0) in three steps 95 times.
<Figure size 864x504 with 0 Axes>
(b) It is still the case that approximately 25% of the time the person needs one step to move one pace to the left of the starting point. This is because there is a probability of 0.25 of stepping to the left on the initial step. However, the Markov chain makes arrival at (-1, 0) in 3 steps more common than before. (It accounts for more like 9% of the trials, rather than 7.5%.) Similarly, taking 5, 7, 9, 11, …, or 999 steps to reach (-1, 0) is also more common. This is because every time the person steps to the right, there is a higher probability of going left (0.4) next, as compared with 0.25 in the non-Markov chain problem. As a result, it is less common (maybe 38% of the time on average rather than 40%) that the position (-1, 0) is not reached within 1000 steps.
Exercise 6: Two people get lost in a shopping mall. They both want to find each other as soon as possible. However, each has no clue where the other one is. There are two strategies available:
(1) One person stays in the same place. The other moves around.
(2) Both people move.
Which strategy is better for them to meet?
Do simulations and explain how they support your answer.
Show code cell source
def meet_one_still(max_iterations, to_plot):
# Keep track of x-coordinates in the array x.
# Keep track of the corresponding y-coordinates in the array y.
x, y = np.zeros(max_iterations), np.zeros(max_iterations)
# Assume a starting position of (10, 0) for the still person.
# Assume a starting point of (0, 0) for the moving person.
x[0] = 0
y[0] = 0
x_target = 0
y_target = 10
found = (x[0] == x_target) and (y[0] == y_target)
i = 1
while (i < max_iterations) and not(found):
val = random.choice(['up', 'down', 'left', 'right'])
# print(val)
if val == 'up':
x[i] = x[i-1]
y[i] = y[i-1] + 1
elif val == 'down':
x[i] = x[i-1]
y[i] = y[i-1] - 1
elif val == 'left':
x[i] = x[i-1] - 1
y[i] = y[i-1]
else: # val == 'right'
x[i] = x[i-1] + 1
y[i] = y[i-1]
# print(x[i],y[i])
if (x[i] == x_target) and (y[i] == y_target):
found = True
i += 1
if i >= max_iterations:
print(f'Target not found in {max_iterations} steps.')
else:
print(f'Target found in {i-1} steps.')
if to_plot:
plt.title(f"{i-1} steps")
plt.plot(x, y, 'r*-')
plt.show()
print(f"Final position")
return x[i-1], y[i-1]
meet_one_still(100_000, True)
Show code cell source
def both_move(max_iterations, to_plot):
# Keep track of x-coordinates in the array x.
# Keep track of the corresponding y-coordinates in the array y.
x, y = np.zeros(max_iterations), np.zeros(max_iterations)
x2, y2 = np.zeros(max_iterations), np.zeros(max_iterations)
# Assume a starting position of (10, 0) for Person 1.
# Assume a starting point of (0, 0) for Person 2.
x[0] = 0
y[0] = 0
x2[0] = 1
y2[0] = 0
not_met = (x[0] != x2[0]) or (y[0] != y2[0])
i = 1
while (i < max_iterations) and not_met:
val = random.choice(['up', 'down', 'left', 'right'])
# print(val)
if val == 'up':
x[i] = x[i-1]
y[i] = y[i-1] + 1
elif val == 'down':
x[i] = x[i-1]
y[i] = y[i-1] - 1
elif val == 'left':
x[i] = x[i-1] - 1
y[i] = y[i-1]
else: # val == 'right'
x[i] = x[i-1] + 1
y[i] = y[i-1]
val2 = random.choice(['up', 'down', 'left', 'right'])
# print(val)
if val2 == 'up':
x2[i] = x2[i-1]
y2[i] = y2[i-1] + 1
elif val == 'down':
x2[i] = x2[i-1]
y2[i] = y2[i-1] - 1
elif val == 'left':
x2[i] = x2[i-1] - 1
y2[i] = y2[i-1]
else: # val == 'right'
x2[i] = x2[i-1] + 1
y2[i] = y2[i-1]
# print(x[i],y[i])
if (x[i] == x2[i]) and (y[i] == y2[i]):
not_met = False
i += 1
if i >= max_iterations:
print(f'Target not found in {max_iterations} steps.')
else:
print(f'Target found in {i-1} steps.')
if to_plot:
plt.title(f"{i-1} steps")
plt.plot(x, y, 'r*-')
plt.show()
print(f"Final position")
return x[i-1], y[i-1]
both_move(100_000, True)
Simulations on two persons that start ten paces apart show that typically the better strategy is for one person to stay in the same place and for the other to move around. Simulations of this strategy usually end with the two people finding each other. Simulations in which both people engage in random walks typically end with them failing to meet within 100,000 steps.
5.9.6. Agent-based models#
Exercise 1: Simulate the spread of information under the given assumptions. How many days does it seem to take in general for the information to spread to half of the population? Will all individuals be informed after a certain number of days?
def rumor_spread(total_population):
# Set a maximum number of iterations.
max_it = 1000
# Inform Agent 0.
informed_status = [1]
# No one else has been informed.
for i in range(total_population-1):
informed_status.append(0)
# Generate a random number from 0 to 5 for each agent and store in a list as the number of transmissions.
transmission_numbers = []
for i in range(total_population):
transmission_numbers.append(random.randint(0, 5))
# Simulation of the process
day = 0
spread_to_half = False
day_spread_to_half = 0
while informed_status.count(1) != total_population and (day < max_it):
# Record the first day that at least half of the population has the information.
if not(spread_to_half) and informed_status.count(1) >= int(total_population/2):
day_spread_to_half = day
spread_to_half = True
new_status = informed_status[:]
for agent_index in range(total_population):
# print(informed_status)
if informed_status[agent_index] == 1: # If agent is informed,
# transmit to (inform) the appropriate number of randomly selected agents (excluding self).
for informing in range(transmission_numbers[agent_index]):
recipient_index = random.randrange(total_population)
while recipient_index == agent_index:
recipient_index = random.randrange(total_population) # Ensure agent does not transmit to self.
new_status[recipient_index] = 1
# Copy the lists to ensure that informed_status and new_status point to two different lists in memory.
informed_status = new_status[:]
day += 1
if informed_status.count(1) == total_population:
print(f"All the individuals are informed by Day {day}.")
else:
print(f"Not all the individuals were informed within the maximum number of iterations ({max_it}).")
if day_spread_to_half > 0:
print(f"(Half of the individuals are informed by Day {day_spread_to_half}.)")
rumor_spread(1000)
Typically it seems to take about 6 days in general for the information to spread to half of the population of 1000 and about 9 days for all individuals to be informed. However, sometimes not all the individuals are informed within a maximum number of iterations, such as 1000. Upon closer inspection (by doing print(informed_status.count(1) upon exiting the while loop), this situation seems to arise when the initial agent is assigned a transmission number of 0.
Show code cell source
def rumor_spread(total_population):
total_population = 1000
# Set a maximum number of iterations.
max_it = 1000
# Inform Agent 0.
informed_status = [1]
# No one else has been informed.
for i in range(total_population-1):
informed_status.append(0)
# Generate a random number from 0 to 5 for each agent and store in a list as the number of transmissions.
transmission_numbers = []
for i in range(total_population):
transmission_numbers.append(random.randint(0, 5))
# Simulation of the process
day = 0
spread_to_half = False
day_spread_to_half = 0
while informed_status.count(1) != total_population and (day < max_it):
# Record the first day that at least half of the population has the information.
if not(spread_to_half) and informed_status.count(1) >= int(total_population/2):
day_spread_to_half = day
spread_to_half = True
new_status = informed_status[:]
for agent_index in range(total_population):
# print(informed_status)
if informed_status[agent_index] == 1: # If agent is informed,
# transmit to (inform) the appropriate number of randomly selected agents (excluding self).
for informing in range(transmission_numbers[agent_index]):
recipient_index = random.randrange(total_population)
while recipient_index == agent_index:
recipient_index = random.randrange(total_population) # Ensure agent does not transmit to self.
new_status[recipient_index] = 1
# Copy the lists to ensure that informed_status and new_status point to two different lists in memory.
informed_status = new_status[:]
day += 1
if day < max_it:
print(f"All the individuals are informed by Day {day}.")
else:
print(f"Not all the individuals were informed within the maximum number of iterations ({max_it}).")
if day_spread_to_half > 0:
print(f"(Half of the individuals are informed by Day {day_spread_to_half}.)")
rumor_spread(1000)
All the individuals are informed by Day 8.
(Half of the individuals are informed by Day 5.)
Typically it seems to take about 6 days in general for the information to spread to half of the population of 1000 and about 8 days for all individuals to be informed. However, sometimes not all the individuals are informed within a maximum number of iterations, such as 1000. This situation arises when the transmission numbers are too low to produce the typical pattern of information spread.
Exercise 2: This agent-based model could also be applied to the spread of disease. If “knowing the information” means “having the disease” and “not having the information” means “not having the disease”, what are the interpretations of the assumptions, initial condition, and parameters that are given? Explain how you may find the model compelling in the context of disease, or what changes to the model you recommend to better reflect the spread of disease.
If a disease is shared, it might spread from one agent to another similarly to how information spreads. We can assume, similarly to before that:
The population is a closed community. The number of individuals does not change. With a disease raging, this assumption may not be sound.
Agents who do not have the disease do not pass the disease to others. This assumption is not good for all diseases. During COVID, we saw that asymptomatic individuals could spread the disease. So people who appeared “not sick” were still contagious.
An agent does not pass the disease to itself.
Once an agent catches the disease, it will not be uninfected. This assumption may not be good, as there should be a transition from “sick” to “not sick”.
A transmission rate defines how many people catch the disease from a given individual in one day.
Each agent has one of the allowed transmission rates with equal probability. It is unclear whether different people have different degrees of contagion.
When an agent spreads the disease to another individual, that individual is selected from all the other members of the population with equal probability. This might be no less contrived than the analogous assumption in the information-spreading model. However, in reality, both cases involve social networks in which some people come into contact with a given individual more than others.
Like for the information spreading, we could impose the initial condition that on Day 0, 1 individual is sick. (This person is called the “index case” in the field.)
For parameters for the agent-based model of disease transmission, we could again say
The value of the population parameter is 1000. (There are 1000 agents.)
The allowed transmission rates are 0, 1, 2, 3, 4, and 5.
The way the disease could spread is as follows: We have Persons 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,…, 1000. These people might have transmission rates 3, 3, 2, 0, 5, 1, 1, 2, 3, 4, 2, 1, …, 4 respectively. Initially, 1 person is sick. If that person is Person 1, and Person 1 has a transmission rate of 3, then on the first day of illness, Person 1 might spread the disease to Persons 5, 8, and 9 with transmission rates 5, 2, and 3, respectively. In Day 2 of the pandemic, Person 1 spreads the information to 3 people, Person 5 to 5 people, Person 8 to 2 people and Person 9 to 3 people. Note these may be some of the same people or people who already are sick in our model. The process continues day-by-day. One of the complicating factors with COVID was that people could spread the disease a couple of days before they showed symptoms themselves. Our model does not account for this.
5.9.7. Mathematical Games#
Exercise 1: For the game of craps, does the choice of “Pass Line” vs. “Don’t Pass” affect the likelihood of winning, under the rules given? If so, what kind of difference and how much difference? Use quantitative information to support your answer. State whether you have provided mathematical proof or computational evidence.
Show code cell source
def roll_two_dice(unbiased):
# Return the sum of a roll of two six-sided dice with a boolean parameter unbiased.
if unbiased:
die1 = random.choice([1, 2, 3, 4, 5, 6])
die2 = random.choice([1, 2, 3, 4, 5, 6])
else:
die1 = random.choice([1, 2, 3, 4, 5, 5, 6, 6])
die2 = random.choice([1, 2, 3, 4, 5, 5, 6, 6])
return die1 + die2
def pass_line(unbiased):
# Play craps with the pass-line rules.
# The boolean parameter allows for both unbiased and biased dice.
# Return -3 for a draw, -2 for a loss, and -1 for a win.
roll = roll_two_dice(unbiased)
if (roll == 7) or (roll == 11):
return -1 # win
elif (roll == 2) or (roll == 3) or (roll == 12):
return -2 # lose
else:
the_point = roll
roll = roll_two_dice(unbiased)
if (roll == the_point):
return -1 # win
elif (roll == 7):
return -2 # lose
else:
return -3 # draw
def dont_pass(unbiased):
# Play craps with the no-pass rules.
# The boolean parameter allows for both unbiased and biased dice.
# Return 1 for a draw, 2 for a loss, and 3 for a win.
roll = roll_two_dice(unbiased)
if (roll == 7) or (roll == 11):
return 2 # lose
elif (roll == 2) or (roll == 3) or (roll == 12):
return 3 # win
else:
the_point = roll
roll = roll_two_dice(unbiased)
if (roll == the_point):
return 2 # lose
elif (roll == 7):
return 3 # win
else:
return 1 # draw
def histogram_craps(trials, unbiased):
# Play craps trials times with pass-line rules and trials times with the no-pass rules.
# The boolean parameter allows for both unbiased and biased dice.
# Draw a histogram with the outcomes.
results = []
for i in range(trials):
results.append(pass_line(unbiased))
results.append(dont_pass(unbiased))
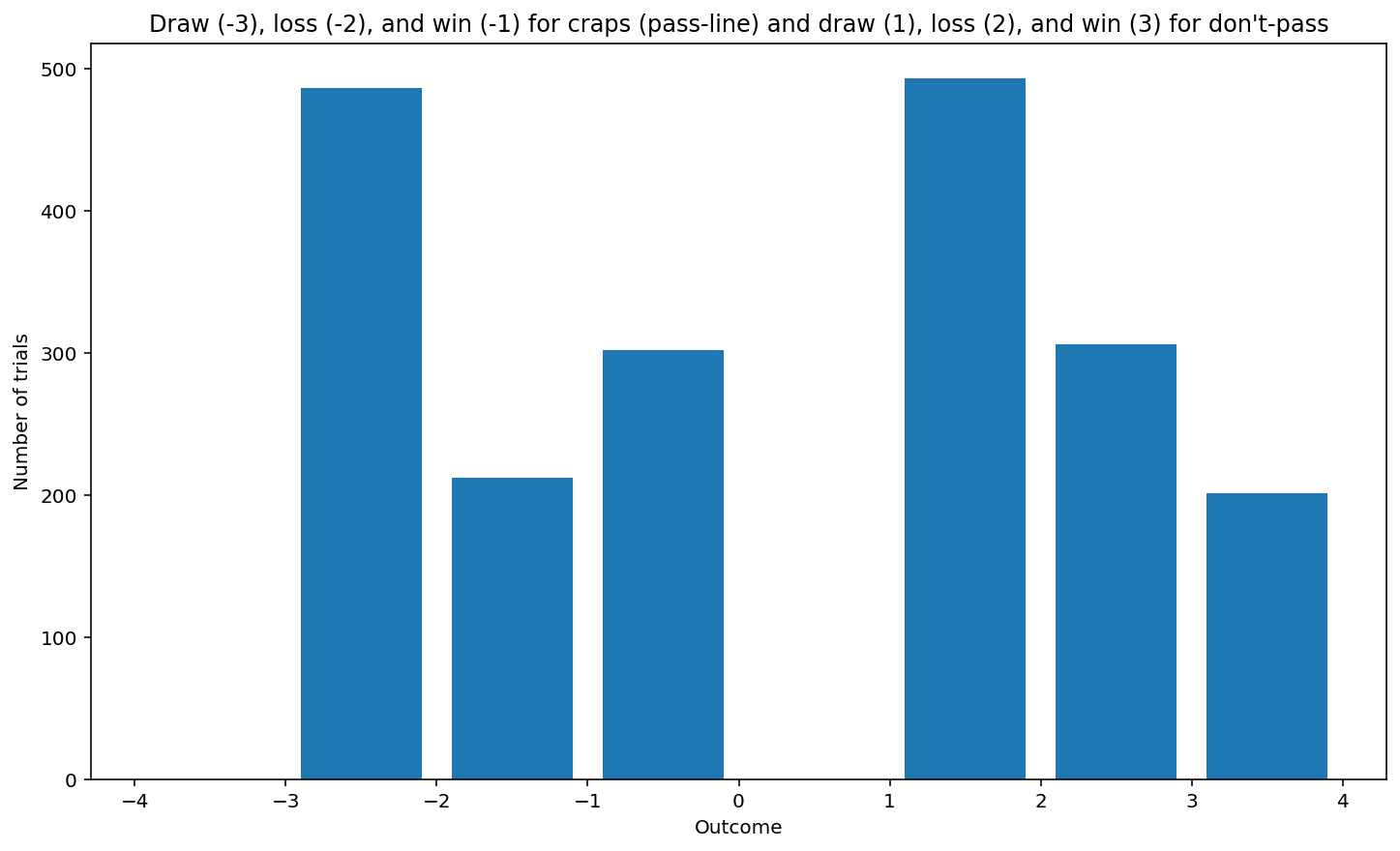
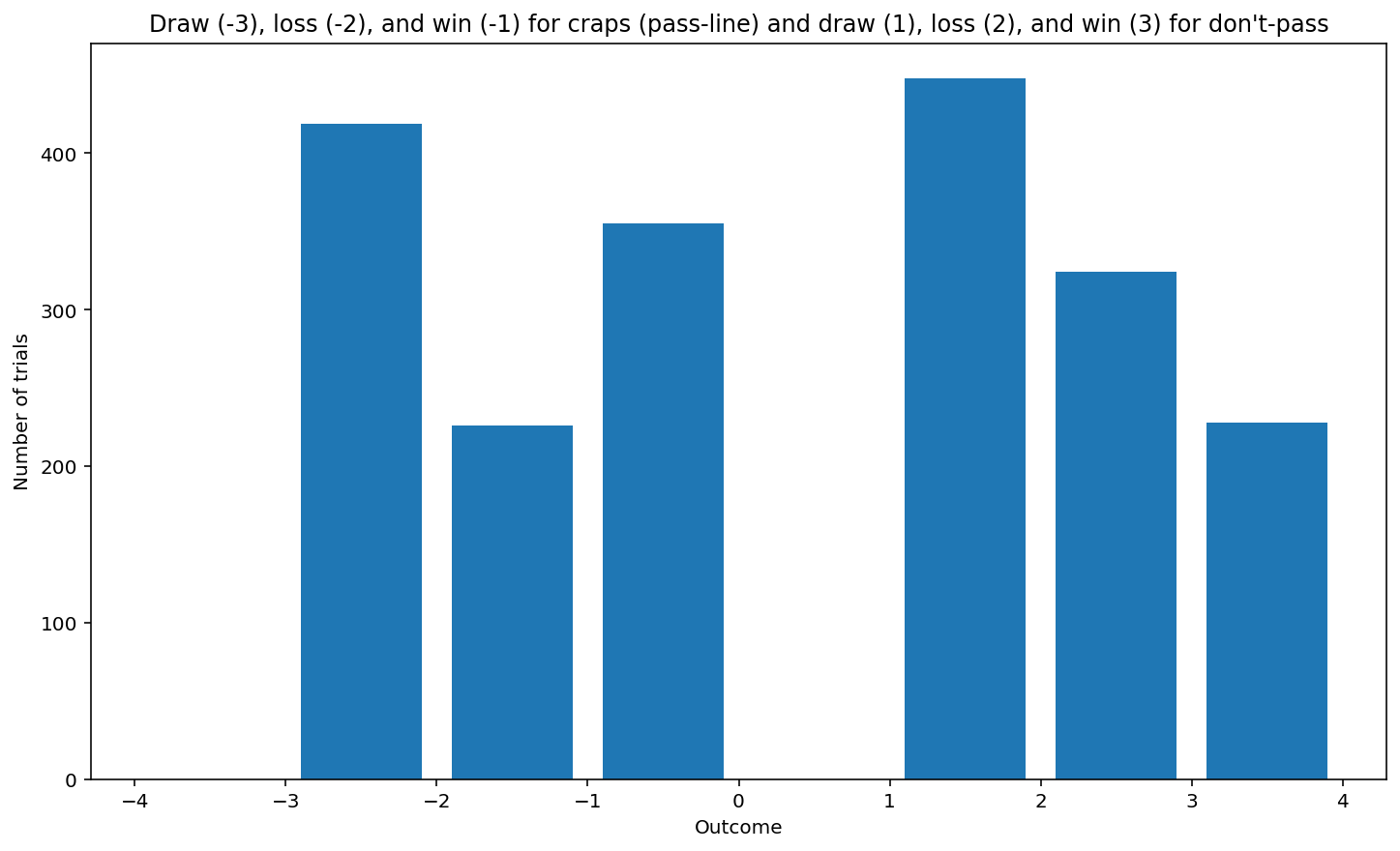
plt.title("Draw (-3), loss (-2), and win (-1) for craps (pass-line) and draw (1), loss (2), and win (3) for don't-pass")
plt.xlabel('Outcome')
plt.ylabel('Number of trials')
plt.hist(results, bins = range(-4, 5), rwidth = 0.8)
plt.figure()
histogram_craps(1000, True)
The results give computational evidence that the “Pass Line” rules are favorable. In both “Pass” and “Don’t Pass” the most common outcome is a draw. But for losses then wins, respectively, we see the third bar higher than the second in the first set of three bars, meaning that there are more wins than loses. The “Don’t Pass” rules make a win less likely than a loss: the third bar is lower than the second in the second set of three bars. It appears that the number of wins for “Pass” are comparable to the number of losses for “Don’t Pass”, and the number of losses for “Pass” are comparable to the number of wins for “Don’t Pass”.
Exercise 2: If one of the two dice is biased in the game of craps, how does that affect the analysis and conclusions from Exercise 1? Illustrate your answer by doing some simulations and discussing the results.
The qualitative comparison between the outcomes of the two versions of the game is quite robust to various biases in the dice for the biases that I tried. There are quantitative changes in the outcomes. For example, a win becomes more likely for don’t pass than before if one of the dice rolls a 5 with probability 1/4, a six with probability 1/4, and a 1, 2, 3, or 4 with probability 1/8 each. However, wins are still more common under the pass-line rules than don’t-pass even in this case. Draws are less frequent than with unbiased dice, but they are still the most frequent outcome.
Exercise 3: Simulate the optimal stopping problem for ten rooms using the algorithm discussed in this section. Execute many trials.
(a) Explain whether you typically get the best room or not when you preview 37% (three or four) of the rooms.
(b) If you don’t get the best room, how good of a room do you typically get?
(c) Show a histogram of the ranks of the rooms you choose. Do the shape, center, and spread of the ranks suggest that the strategy (algorithm) is a good one for winning the best room? Explain.
(d) Does the strategy of previewing three or four of the ten rooms tend to lead to a better outcome than if you preview two or five? Support your answer.
Show code cell source
def trials_of_room_visits(num_trials, num_rooms_per_trial, fraction_to_preview):
# Keep track of the rank of the room chosen in each trial.
ranks_chosen = []
# Keep track of how many times you chose the best, second best, third best, and worst room.
rank1 = 0
rank2 = 0
rank3 = 0
rank_last = 0
for i in range(num_trials):
# For each trial, generate a list of ratings between 0 and 100 inclusive.
ratings = []
for i in range(num_rooms_per_trial):
ratings.append(random.randint(0, 100))
number_to_visit = int(fraction_to_preview * num_rooms_per_trial)
# Visit the first 37% of rooms.
# Find the max among the first 37%.
max = ratings[0]
for i in range(number_to_visit):
if ratings[i] > max:
max = ratings[i]
# Advance to the next room.
i += 1
# While rooms still remain to be visited,
# and the rating does not surpass the first 37% of ratings,
while (i < num_rooms_per_trial) and (ratings[i] <= max):
# advance to the next room.
i += 1
# If you haven't seen the final room,
if i < num_rooms_per_trial:
# you must have found an room that surpasses the first 37%.
choice = ratings[i]
else: # Otherwise, you must take the last room.
choice = ratings[num_rooms_per_trial-1]
ratings.sort(reverse = True)
rank = ratings.index(choice) + 1
ranks_chosen.append(rank)
if rank == 1:
rank1 += 1
elif rank == 2:
rank2 += 1
elif rank == 3:
rank3 += 1
elif rank == num_rooms_per_trial:
rank_last += 1
plt.title(f"Number of times rooms of each rank were chosen for {num_rooms_per_trial} rooms and {num_trials} trials when {fraction_to_preview} of the rooms were previewed")
plt.xlabel('Rank')
plt.ylabel('Number of trials')
plt.hist(ranks_chosen, bins = num_rooms_per_trial, rwidth = 0.8)
# print(ranks_chosen)
print(f'Number of rooms: {num_rooms_per_trial}')
print(f'Number of rooms previewed: {number_to_visit}')
print(f'Number of trials with {num_rooms_per_trial} rooms per trial: {num_trials}')
print(f'Percent of times best room was picked: {round(rank1/num_trials * 100)}')
print(f'Percent of times second best room was picked: {round(rank2/num_trials * 100)}')
print(f'Percent of times third best room was picked: {round(rank3/num_trials * 100)}')
print(f'Percent of times one of the top three rooms was picked: {round((rank1 + rank2 + rank3)/num_trials * 100)}')
print(f'Percent of times worst room was picked: {round(rank_last/num_trials * 100)}')
trials_of_room_visits(1000, 10, 0.37)
Number of rooms: 10
Number of rooms previewed: 3
Number of trials with 10 rooms per trial: 1000
Percent of times best room was picked: 41
Percent of times second best room was picked: 19
Percent of times third best room was picked: 10
Percent of times one of the top three rooms was picked: 71
Percent of times worst room was picked: 3
(a) When you preview three of the rooms, you get the best room about 41% of the time, which is a lot better than a random choice of \(1/n = 1/10\).
(b) You typically get a room in the top three about 70% of the time—about 20% of the time you get the second best and about 10% of the time you get third best.
(c) The histogram suggests that the strategy (algorithm) is a good one for winning the best room because it shows that Rank 1 is the dominant rank selected, and lower and lower ranks are generally chosen less and less often.
Show code cell source
trials_of_room_visits(1000, 10, 0.2)
Number of rooms: 10
Number of trials with 10 rooms per trial: 1000
Percent of times best room was picked: 38
Percent of times second best room was picked: 21
Percent of times third best room was picked: 12
Percent of times one of the top three rooms was picked: 72
Percent of times worst room was picked: 3
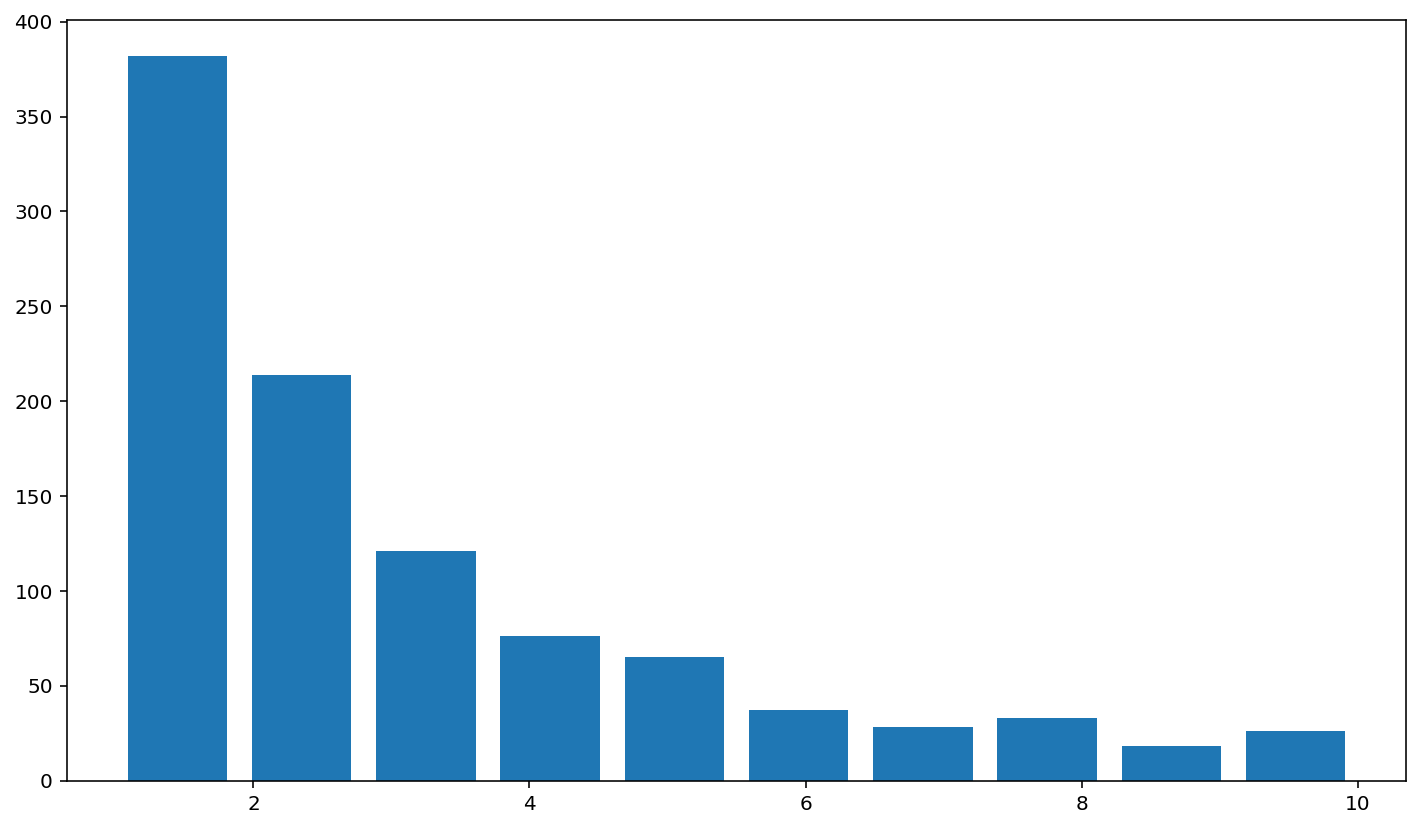
trials_of_room_visits(1000, 10, 0.5)
Number of rooms: 10
Number of trials with 10 rooms per trial: 1000
Percent of times best room was picked: 36
Percent of times second best room was picked: 14
Percent of times third best room was picked: 9
Percent of times one of the top three rooms was picked: 60
Percent of times worst room was picked: 6
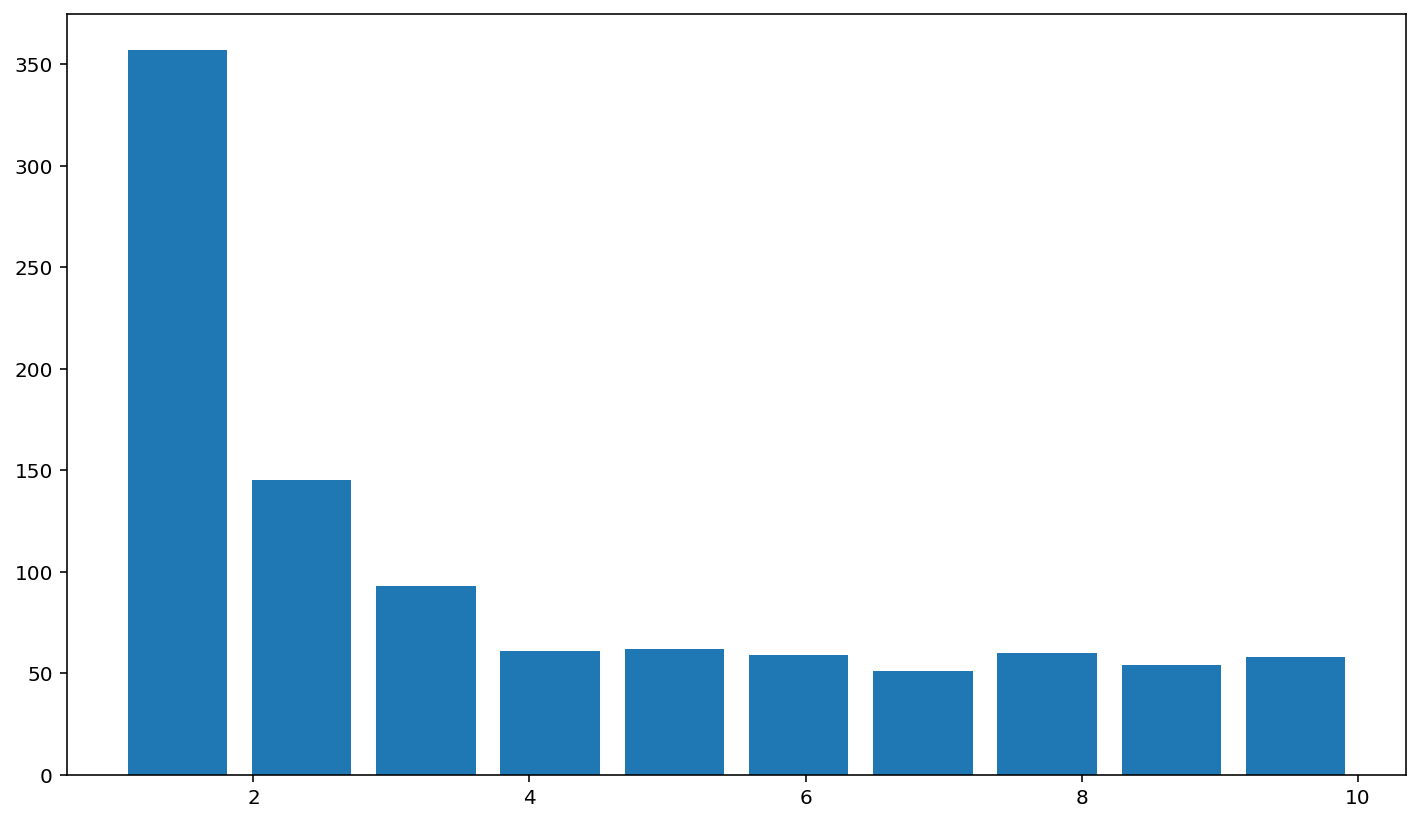
(d) The strategy of previewing three of the ten rooms tends to lead to a better outcome than if you preview a fraction 0.2 of the rooms (two rooms) or 0.4 of the rooms (four rooms). With a preview of two rooms, the percentage of times that you get the best room drops slightly compared to a preview of three rooms. The percentage of times you get a room in the top three seems to hold fairly steady. With a preview of four rooms, the percentage of times that you get the best room drops a little compared to a preview of three rooms. The percentage of times you get a room in the top three drops quite noticeably. With a preview of four rooms, the histogram shows a slightly lower peak at Rank 1 and a thicker tail for the distribution, meaning lower-rank choices are more common.
(e) These results are generally consistent with the mathematical finding that the optimal fraction of the total rooms that you should preview is \(1/e\) because \(1/e\) is between 30 and 40% of the rooms. Technically, this mathematical conclusion only applies as \(n\) gets very large, so it is striking that even when \(n\) is only 10, we should still preview around 37% of the rooms. If the probability that you will select the best room this way tends to \(1/e\) for large \(n\), then we would predict obtaining the best room about 37% of the time. Our simulations show slightly better results than that when we preview three or four out of the ten rooms. It’s reasonable to imagine that getting the best room might become harder as \(n\) gets large, so probably if we simulate with a larger number of rooms and preview about 37% of them, we might get the best room only about 37% of the time, rather than 40 or 41%.
Exercise 4: With a fair coin, is there a winning strategy to maximize your points in the coin-flipping game described in this section? If so, what is the winning strategy? Illustrate your conclusions using simulation.
Exercise 5: If you know the coin is biased, with 60% chance of heads and 40% chance of tails, how should you change your strategy? Illustrate your answer using simulation.
Show code cell source
def flipping_game(prob_heads, token_count, F, max_turns_per_game, trials):
'''Suppose you have a coin that flips heads with probability prob_heads and token_count tokens.
Put a fraction F of your tokens (F * token_count tokens) on the table, 0 < F <= 1.
Then flip the coin.
If it comes up heads, then you win F * token_count additional tokens.
Otherwise, you lose all F * token_count tokens.
Repeat the process until you lose all your tokens or up to a maximum number of turns per game, whichever comes first.
Note your score may involve fractions of tokens (points).
Do trials trials.'''
if F > 1 or F <= 0:
print("ERROR. Choose 0 < F <= 1.")
initial_tokens = token_count
final_points = [] # Final points for each trial of the game
less_than_1_point = 0 # Number of times the final points were less than 1
less_than_starting_points = 0 # Number of times for the final points were less than the initial number
final_points_losses = [] # Final points for each game with a score < initial points
final_points_wins = [] # Final points for each game with a score >= initial points
for i in range(trials):
turns = 0
token_count = initial_tokens
while (token_count > 0) and (turns <= max_turns_per_game):
r = random.uniform(0, 1)
if r < prob_heads:
token_count += F * token_count
else:
token_count -= F * token_count
turns += 1
if token_count < 1:
less_than_1_point += 1
final_points_losses.append(token_count)
elif token_count < initial_tokens:
less_than_starting_points += 1
final_points_losses.append(token_count)
else:
final_points_wins.append(token_count)
final_points.append(token_count)
total_loss_percentage = round(less_than_1_point/trials*100)
non_zero_loss_percentage = round(less_than_starting_points/trials*100)
print(f"Game ended with 0 <= points < 1 approximately {total_loss_percentage}% of the time within a maximum number of turns = {max_turns_per_game}.")
print(f"Game ended with 1 <= points <= {initial_tokens} initial tokens approximately {non_zero_loss_percentage}% of the time.")
print(f"So, the player won additional tokens approximately {100 - total_loss_percentage - non_zero_loss_percentage}% of the time.")
print(f"The average loss between 1 and 100 across all trials is approximately {initial_tokens - round(sum(final_points_losses)/len(final_points_losses))} points.")
print(f"The average winnings (meaning average number of final_points beyond the initial 100) across all trials is approximately {round(sum(final_points_wins)/len(final_points_wins))-100}.")
print(f"Maximum score was approximately {round(max(final_points))} in {trials} trials.")
flipping_game(0.5, 100, 0.5, 30, 10_000)
Game ended with 0 <= points < 1 approximately 50% of the time within a maximum number of turns = 30.
Game ended with 1 <= points <= 100 initial tokens approximately 42% of the time.
So, the player won additional tokens approximately 8% of the time.
The average loss between 1 and 100 across all trials is approximately 93 points.
The average winnings (meaning average number of final_points beyond the initial 100) across all trials is approximately 910.
Maximum score was approximately 39455 in 10000 trials.
With a fair coin, the formula in the chapter says the optimal \(F\) is 0, meaning that there is no winning strategy to maximize your points in the coin-flipping game described in this section. The simulation shows that about 50% of the time you lose all your tokens (100 tokens) within the maximum number of turns in the game (30). You end the game with more points than you started with only about 8% of the time. Note that you consistently lose 93 of your 100 tokens when you lose. The average winnings when you do win tend to be about 1000 tokens. The number of points you have at the end can occasionally be very large. A high score is possible but improbable, within this strategy that I do not consider a winning strategy.
Exercise 5: If you know the coin is biased, with probability 0.6 of success, the formula in the chapter says you should use \(F = 0.2\).
flipping_game(0.6, 100, 0.2, 30, 10_000)
Game ended with 0 <= points < 1 approximately 0% of the time within a maximum number of turns = 30.
Game ended with 1 <= points <= 100 initial tokens approximately 34% of the time.
So, the player won additional tokens approximately 66% of the time.
The average loss between 1 and 100 across all trials is approximately 36 points.
The average winnings (meaning average number of final_points beyond the initial 100) across all trials is approximately 382.
Maximum score was approximately 8440 in 10000 trials.
This strategy has a very different outcome. When we play the game this way, we never seem to lose all the tokens (instead of losing all of them half the time). Your winnings are less on average (around 380) this way than with the fair coin and \(F = 1/2\). However, you have more points at the end that at the beginning far more often— around 66% of the time rather than 8%. When you do lose, the losses are less on average (35 points, rather than 93 points).